Harmonic functions | Integral transforms | Signal processing | Singular integrals
Hilbert transform
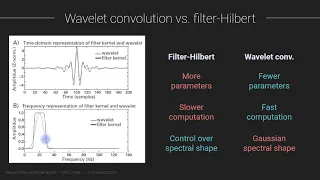
In mathematics and in signal processing, the Hilbert transform is a specific linear operator that takes a function, u(t) of a real variable and produces another function of a real variable H(u)(t). This linear operator is given by convolution with the function (see ). The Hilbert transform has a particularly simple representation in the frequency domain: It imparts a phase shift of ±90° (π⁄2 radians) to every frequency component of a function, the sign of the shift depending on the sign of the frequency (see ). The Hilbert transform is important in signal processing, where it is a component of the analytic representation of a real-valued signal u(t). The Hilbert transform was first introduced by David Hilbert in this setting, to solve a special case of the Riemann–Hilbert problem for analytic functions. (Wikipedia).