
Convolution Theorem: Fourier Transforms
Free ebook https://bookboon.com/en/partial-differential-equations-ebook Statement and proof of the convolution theorem for Fourier transforms. Such ideas are very important in the solution of partial differential equations.
From playlist Partial differential equations

Differential Equations | Convolution: Definition and Examples
We give a definition as well as a few examples of the convolution of two functions. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Differential Equations

Example of Convolution Theorem: f(t)=t, g(t)=sin(t)
ODEs: Verify the Convolution Theorem for the Laplace transform when f(t) = t and g(t) = sin(t). The Convolution Theorem states that L(f*g) = L(f) . L(g); that is, the Laplace transform of a convolution is the product of the Laplace transforms.
From playlist Differential Equations

Math 139 Fourier Analysis Lecture 05: Convolutions and Approximation of the Identity
Convolutions and Good Kernels. Definition of convolution. Convolution with the n-th Dirichlet kernel yields the n-th partial sum of the Fourier series. Basic properties of convolution; continuity of the convolution of integrable functions.
From playlist Course 8: Fourier Analysis

Proof of the Convolution Theorem
Proof of the Convolution Theorem, The Laplace Transform of a convolution is the product of the Laplace Transforms, changing order of the double integral, proving the convolution theorem, www.blackpenredpen.com
From playlist Convolution & Laplace Transform (Nagle Sect7.7)

Concavity and Parametric Equations Example
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Concavity and Parametric Equations Example. We find the open t-intervals on which the graph of the parametric equations is concave upward and concave downward.
From playlist Calculus

In this video, I provide some intuition behind the concept of convolution, and show how the convolution of two functions is really the continuous analog of polynomial multiplication. Enjoy!
From playlist Real Analysis

Learn to determine the value that makes the piecewise function continuous
👉 Learn how to find the value that makes a function continuos. A function is said to be continous if two conditions are met. They are: the limit of the function exist and that the value of the function at the point of continuity is defined and is equal to the limit of the function. To find
From playlist The Limit

The Convolution of Two Functions | Definition & Properties
We can add two functions or multiply two functions pointwise. However, the convolution is a new operation on functions, a new way to take two functions and combine them. In this video we define the convolution of two functions, state and prove several of its nice algebraic properties, and
From playlist Fourier

Pablo Shmerkin: Additive combinatorics methods in fractal geometry - lecture 2
In the last few years ideas from additive combinatorics were applied to problems in fractal geometry and led to progress on some classical problems, particularly on the smoothness of Bernoulli convolutions and other self-similar measures. We will introduce some of these tools from additive
From playlist Combinatorics

PROGRAM NAME :WINTER SCHOOL ON STOCHASTIC ANALYSIS AND CONTROL OF FLUID FLOW DATES Monday 03 Dec, 2012 - Thursday 20 Dec, 2012 VENUE School of Mathematics, Indian Institute of Science Education and Research, Thiruvananthapuram Stochastic analysis and control of fluid flow problems have
From playlist Winter School on Stochastic Analysis and Control of Fluid Flow

Lecture 10 | The Fourier Transforms and its Applications
Lecture by Professor Brad Osgood for the Electrical Engineering course, The Fourier Transforms and its Applications (EE 261). Professor Osgood introduces the final operation of convolution to the central limit theorem. The Fourier transform is a tool for solving physical problems. In t
From playlist Fourier

Video5-18: Convolution Theorem, proof, examples, application. Elementary differential equations
Elementary differential equations Video5-18: Convolution Theorem, proof, examples with applications to IVP. Course playlist: https://www.youtube.com/playlist?list=PLbxFfU5GKZz0GbSSFMjZQyZtCq-0ol_jD
From playlist Elementary Differential Equations

Pablo Shmerkin: Additive combinatorics methods in fractal geometry - lecture 1
In the last few years ideas from additive combinatorics were applied to problems in fractal geometry and led to progress on some classical problems, particularly on the smoothness of Bernoulli convolutions and other self-similar measures. We will introduce some of these tools from additive
From playlist Combinatorics

Combinatorial Theorems in Random Sets - David Conlon
David Conlon University of Cambridge November 22, 2010 The famous theorem of Szemerédi says that for any natural number kk and any a greater than 0a greater than 0 there exists n such that if N greater than or =nN greater to or =n then any subset AA of the set [N]=1,2,...,N[N]=1,2,...,N o
From playlist Mathematics

Convolution as spectral multiplication
This video lesson is part of a complete course on neuroscience time series analyses. The full course includes - over 47 hours of video instruction - lots and lots of MATLAB exercises and problem sets - access to a dedicated Q&A forum. You can find out more here: https://www.udemy.
From playlist NEW ANTS #3) Time-frequency analysis

Video5-17: Convolution Theorem, examples of convolution. Elementary differential equations
Elementary differential equations Video5-17: Convolution Theorem, examples of convolution; graphic interpretation. Course playlist: https://www.youtube.com/playlist?list=PLbxFfU5GKZz0GbSSFMjZQyZtCq-0ol_jD
From playlist Elementary Differential Equations

Michael Elad: "Sparse Modeling in Image Processing and Deep Learning"
New Deep Learning Techniques 2018 "Sparse Modeling in Image Processing and Deep Learning" Michael Elad, Technion - Israel Institute of Technology, Computer Science Abstract: Sparse approximation is a well-established theory, with a profound impact on the fields of signal and image proces
From playlist New Deep Learning Techniques 2018
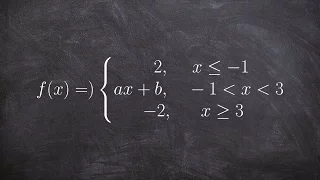
Find the value makes a piecewise function continuous with system of equations
👉 Learn how to find the value that makes a function continuos. A function is said to be continous if two conditions are met. They are: the limit of the function exist and that the value of the function at the point of continuity is defined and is equal to the limit of the function. To find
From playlist The Limit