
Definition of a group Lesson 24
In this video we take our first look at the definition of a group. It is basically a set of elements and the operation defined on them. If this set of elements and the operation defined on them obey the properties of closure and associativity, and if one of the elements is the identity el
From playlist Abstract algebra

What is a Group? | Abstract Algebra
Welcome to group theory! In today's lesson we'll be going over the definition of a group. We'll see the four group axioms in action with some examples, and some non-examples as well which violate the axioms and are thus not groups. In a fundamental way, groups are structures built from s
From playlist Abstract Algebra

Now that we know what a quotient group is, let's take a look at an example to cement our understanding of the concepts involved.
From playlist Abstract algebra

A group is (in a sense) the simplest structure in which we can do the familiar tasks associated with "algebra." First, in this video, we review the definition of a group.
From playlist Modern Algebra - Chapter 15 (groups)

Definition of a Group and Examples of Groups
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Definition of a Group and Examples of Groups
From playlist Abstract Algebra

Now that we have defined and understand quotient groups, we need to look at product groups. In this video I define the product of two groups as well as the group operation, proving that it is indeed a group.
From playlist Abstract algebra

Group Definition (expanded) - Abstract Algebra
The group is the most fundamental object you will study in abstract algebra. Groups generalize a wide variety of mathematical sets: the integers, symmetries of shapes, modular arithmetic, NxM matrices, and much more. After learning about groups in detail, you will then be ready to contin
From playlist Abstract Algebra

In this video, you’ll learn how to join groups on LinkedIn. Visit https://edu.gcfglobal.org/en/linkedin/keeping-up-with-linkedin/1/ for our text-based lesson. We hope you enjoy!
From playlist LinkedIn

Abstract Algebra | Definition of a Group and Basic Examples
We present the definition of a group and give a few basic example s of abelian groups. http://www.michael-penn.net
From playlist Abstract Algebra

Chemistry 107. Inorganic Chemistry. Lecture 02
UCI Chemistry: Inorganic Chemistry (Fall 2014) Lec 02. Inorganic Chemistry -- Symmetry and Point Groups View the complete course: http://ocw.uci.edu/courses/chem_107_inorganic_chemistry.html Instructor: Matthew D. Law License: Creative Commons CC-BY-SA Terms of Use: http://ocw.uci.edu/inf
From playlist Chem 107: Week 1
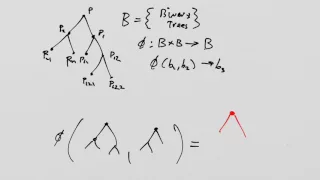
What is a Tensor? Lesson 19: Algebraic Structures I
What is a Tensor? Lesson 19: Algebraic Structures Part One: Groupoids to Fields This is a redo or a recently posted lesson. Same content, a bit cleaner. Algebraic structures are frequently mentioned in the literature of general relativity, so it is good to understand the basic lexicon of
From playlist What is a Tensor?

Lie groups: Positive characteristic is weird
This lecture is part of an online graduate course on Lie groups. We give several examples to show that, over fields of positive characteristic, Lie algebras can behave strangely, and have a weaker connection to Lie groups. In particular the Lie algebra does not generate the ring of all in
From playlist Lie groups
Calista Bernard - Applications of twisted homology operations for E_n-algebras
An E_n-algebra is a space equipped with a multiplication that is commutative up to homotopy. Such spaces arise naturally in geometric topology, number theory, and mathematical physics; some examples include classifying spaces of braid groups, spaces of long knots, and classifying spaces of
From playlist École d'Été 2022 - Cohomology Geometry and Explicit Number Theory

Markus Haase : Operators in ergodic theory - Lecture 3 : Compact semigroups and splitting theorems
Abstract : The titles of the of the individual lectures are: 1. Operators dynamics versus base space dynamics 2. Dilations and joinings 3. Compact semigroups and splitting theorems Recording during the thematic meeting : "Probabilistic Aspects of Multiple Ergodic Averages " the December 8
From playlist Dynamical Systems and Ordinary Differential Equations

Nicola Garofalo: Hypoelliptic operators and analysis on Carnot-Carathéodory spaces
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Algebraic and Complex Geometry

Algebra 1M - international Course no. 104016 Dr. Aviv Censor Technion - International school of engineering
From playlist Algebra 1M

Introduction to Algebraic Theory of Quandles (Lecture - 1) by Valeriy Bardakov
PROGRAM KNOTS THROUGH WEB (ONLINE) ORGANIZERS: Rama Mishra, Madeti Prabhakar, and Mahender Singh DATE & TIME: 24 August 2020 to 28 August 2020 VENUE: Online Due to the ongoing COVID-19 pandemic, the original program has been canceled. However, the meeting will be conducted through onl
From playlist Knots Through Web (Online)

Anton Savin: Index problem for elliptic operators associated with group actions and ncg
Given a group action on a manifold, there is an associated class of operators represented as linear combinations of differential operators and shift operators along the orbits. Operators of this form appear in noncommutative geometry and mathematical physics when describing nonlocal phenom
From playlist HIM Lectures: Trimester Program "Non-commutative Geometry and its Applications"

Abstract Algebra: Motivation for the definition of a group
The definition of a group is very abstract. We motivate this definition with a simple, concrete example from basic algebra. Be sure to subscribe so you don't miss new lessons from Socratica: http://bit.ly/1ixuu9W ♦♦♦♦♦♦♦♦♦♦ Ways to support our channel: ► Join our Patreon : https:/
From playlist Abstract Algebra