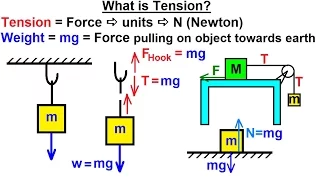
Geometric rigidity
In discrete geometry, geometric rigidity is a theory for determining if a (GCS) has finitely many -dimensional solutions, or , in some metric space. A framework of a GCS is rigid in -dimensions, for a given if it is an isolated solution of the GCS, factoring out the set of trivial motions, or isometric group, of the metric space, e.g. translations and rotations in Euclidean space. In other words, a rigid framework of a GCS has no nearby framework of the GCS that is reachable via a non-trivial continuous motion of that preserves the constraints of the GCS. Structural rigidity is another theory of rigidity that concerns generic frameworks, i.e., frameworks whose rigidity properties are representative of all frameworks with the same . Results in geometric rigidity apply to all frameworks; in particular, to non-generic frameworks. Geometric rigidity was first explored by Euler, who conjectured that all polyhedra in -dimensions are rigid. Much work has gone into proving the conjecture, leading to many interesting results discussed below. However, a counterexample was eventually found. There are also some generic rigidity results with no combinatorial components, so they are related to both geometric and structural rigidity. (Wikipedia).