
Introduces notation and formulas for exponential growth models, with solutions to guided problems.
From playlist Discrete Math

(ML 16.7) EM for the Gaussian mixture model (part 1)
Applying EM (Expectation-Maximization) to estimate the parameters of a Gaussian mixture model. Here we use the alternate formulation presented for (unconstrained) exponential families.
From playlist Machine Learning

We propose a sparse regression method capable of discovering the governing partial differential equation(s) of a given system by time series measurements in the spatial domain. The regression framework relies on sparsity promoting techniques to select the nonlinear and partial derivative
From playlist Research Abstracts from Brunton Lab

Generalized Linear Model (Part A)
Regression Analysis by Dr. Soumen Maity,Department of Mathematics,IIT Kharagpur.For more details on NPTEL visit http://nptel.ac.in
From playlist IIT Kharagpur: Regression Analysis | CosmoLearning.org Mathematics

Mixture Models 4: multivariate Gaussians
Full lecture: http://bit.ly/EM-alg We generalise the equations for the case of a multivariate Gaussians. The main difference from the previous video (part 2) is that instead of a scalar variance we now estimate a covariance matrix, using the same posteriors as before.
From playlist Mixture Models

(ML 16.6) Gaussian mixture model (Mixture of Gaussians)
Introduction to the mixture of Gaussians, a.k.a. Gaussian mixture model (GMM). This is often used for density estimation and clustering.
From playlist Machine Learning

10g Machine Learning: Isotonic Regression
Lecture on isotonic regression. Introduces the idea of a piece-wise linear model with monotonic constraint. Follow along with the demonstration workflow: https://github.com/GeostatsGuy/PythonNumericalDemos/blob/master/SubsurfaceDataAnalytics_IsotonicRegression.ipynb
From playlist Machine Learning
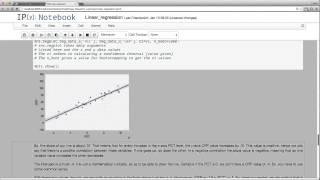
Linear regression is used to compare sets or pairs of numerical data points. We use it to find a correlation between variables.
From playlist Learning medical statistics with python and Jupyter notebooks

Statistical Learning: 7.4 Generalized Additive Models and Local Regression
Statistical Learning, featuring Deep Learning, Survival Analysis and Multiple Testing You are able to take Statistical Learning as an online course on EdX, and you are able to choose a verified path and get a certificate for its completion: https://www.edx.org/course/statistical-learning
From playlist Statistical Learning

Alison Etheridge & Nick Barton: Applying the infinitesimal model
The infinitesimal model is based on the assumption that, conditional on the pedigree, the joint distribution of trait values is multivariate normal, then, selecting parents does not alter the variance amongst offspring. We explain how the infinitesimal model extends to include dominance as
From playlist Probability and Statistics

Andrew Ahn (Columbia) -- Airy edge fluctuations in random matrix sums
In this talk, we discuss a novel integrable probability approach to access edge fluctuations in sums of unitarily invariant Hermitian matrices. We focus on a particular regime where the number of summands is large (but fixed) under which the Airy point process appears. The approach is base
From playlist Columbia Probability Seminar

Kaggle Reading Group: Deep Learning for Symbolic Mathematics (Part 2) | Kaggle
This week we'll continue with "Deep Learning for Symbolic Mathematics", (anonymous, submitted to ICLR 2020). You can find a link to the paper here: https://openreview.net/forum?id=S1eZYeHFDS SUBSCRIBE: https://www.youtube.com/c/kaggle?sub_... About Kaggle: Kaggle is the world's largest c
From playlist Kaggle Reading Group | Kaggle

Matrix Models, Gauge-Gravity Duality, and Simulations on the Lattice (Lecture 2) by Georg Bergner
NONPERTURBATIVE AND NUMERICAL APPROACHES TO QUANTUM GRAVITY, STRING THEORY AND HOLOGRAPHY (HYBRID) ORGANIZERS: David Berenstein (University of California, Santa Barbara, USA), Simon Catterall (Syracuse University, USA), Masanori Hanada (University of Surrey, UK), Anosh Joseph (IISER Mohal
From playlist NUMSTRING 2022

Introduction to quantitative genetics..... by Maria Orive
ORGANIZERS : Deepa Agashe and Kavita Jain DATE & TIME : 05 March 2018 to 17 March 2018 VENUE : Ramanujan Lecture Hall, ICTS Bangalore No living organism escapes evolutionary change. Evolutionary biology thus connects all biological disciplines. To understand the processes drivin
From playlist Third Bangalore School on Population Genetics and Evolution

Stanford Seminar - ML Explainability Part 2 I Inherently Interpretable Models
Professor Hima Lakkaraju presents some of the latest advancements in machine learning models that are inherently interpretable such as rule-based models, risk scores, generalized additive models and prototype based models. View the full playlist: https://www.youtube.com/playlist?list=PLoR
From playlist Stanford Seminars

Segev Wasserkug - Democratizing Optimization Modeling: Status, Challenges, and Future Directions
Recorded 28 February 2023. Segev Wasserkug of IBM Research, Israel, presents "Democratizing Optimization Modeling: Status, Challenges, and Future Directions" at IPAM's Artificial Intelligence and Discrete Optimization Workshop. Note: IBM does not endorse any third parties referenced in the
From playlist 2023 Artificial Intelligence and Discrete Optimization

C07 Homogeneous linear differential equations with constant coefficients
An explanation of the method that will be used to solve for higher-order, linear, homogeneous ODE's with constant coefficients. Using the auxiliary equation and its roots.
From playlist Differential Equations

22. Structure of set addition II: groups of bounded exponent and modeling lemma
MIT 18.217 Graph Theory and Additive Combinatorics, Fall 2019 Instructor: Yufei Zhao View the complete course: https://ocw.mit.edu/18-217F19 YouTube Playlist: https://www.youtube.com/playlist?list=PLUl4u3cNGP62qauV_CpT1zKaGG_Vj5igX Prof. Zhao explains the Ruzsa covering lemma and uses it
From playlist MIT 18.217 Graph Theory and Additive Combinatorics, Fall 2019

