
Reference: Differential Geometry by Do Carmo My first video! Thank you for coming and any suggestion is very welcomed! #some2
From playlist Summer of Math Exposition 2 videos

Gauss's view of curvature and the Theorema Egregium | Differential Geometry 35 | NJ Wildberger
In this video we discuss Gauss's view of curvature in terms of the derivative of the Gauss-Rodrigues map (the image of a unit normal N) into the unit sphere, and expressed in terms of the coefficients of the first and second fundamental forms. We have a look at these equations for the spec
From playlist Differential Geometry

F. Schulze - Mean curvature flow with generic initial data (version temporaire)
Mean curvature flow is the gradient flow of the area functional and constitutes a natural geometric heat equation on the space of hypersurfaces in an ambient Riemannian manifold. It is believed, similar to Ricci Flow in the intrinsic setting, to have the potential to serve as a tool to app
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics
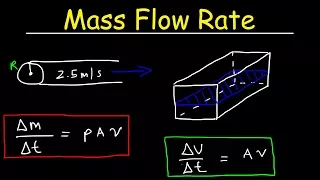
Volume Flow Rate & Mass Flow Rate - Fluid Dynamics Physics Problems
This physics video tutorial provides a basic introduction into mass flow rate and volume flow rate. The mass flow rate is the change in mass per unit time. It is also equal to the product of the fluid density, cross sectional area and the speed of the fluid in a pipe. The volume flow ra
From playlist New Physics Video Playlist

Geometry of the Flow | Lecture 3 | Flow Around a Cylinder
Geometry of the two-dimensional flow around a cylinder. Join me on Coursera: https://www.coursera.org/learn/mathematics-engineers-capstone Lecture notes at https://www.math.hkust.edu.hk/~machas/flow-around-a-cylinder.pdf Subscribe to my channel: http://www.youtube.com/user/jchasnov?sub_
From playlist Flow Around a Cylinder

Lecture 17: Discrete Curvature II (Discrete Differential Geometry)
Full playlist: https://www.youtube.com/playlist?list=PL9_jI1bdZmz0hIrNCMQW1YmZysAiIYSSS For more information see http://geometry.cs.cmu.edu/ddg
From playlist Discrete Differential Geometry - CMU 15-458/858

Physics: Fluid Dynamics: Fluid Flow (1.6 of 7) Bernoulli's Equation Derived
Visit http://ilectureonline.com for more math and science lectures! In this video I will show you how to use Bernoulli's equation to find the pressure and velocity of a fluid in a pipe of various diameters. Next video in this series can be seen at: https://youtu.be/VA03j6t5F-8
From playlist PHYSICS 34 FLUID DYNAMICS

Ben Andrews: Limiting shapes of fully nonlinear flows of convex hypersurfaces
Abstract: I will discuss some questions about the long-time behaviour of hypersurfaces evolving by functions of curvature which are homogeneous of degree greater than 1. ------------------------------------------------------------------------------------------------------------------------
From playlist MATRIX-SMRI Symposium: Singularities in Geometric Flows

Kyeongsu Choi: Translating flows by sub-affine-critical powers of Gauss curvature
Abstract: The Gauss curvature flow with sub-affine-critical powers generically develops Type II singularities, while the flow with super-affine-critical powers converges to the round point. Therefore, to analyze the singularities with small powers, one needs to the translators as the model
From playlist MATRIX-SMRI Symposium: Singularities in Geometric Flows

Bernoulli's Equation for Fluid Flow Video in Physics
Bernoulli's Equation for Fluid Flow Video in Physics. Thanks to Jacob Bowman for making this video for my channel!
From playlist Physics

(Non)uniqueness questions in mean curvature flow - Lu Wang
Variational Methods in Geometry Seminar Topic: (Non)uniqueness questions in mean curvature flow Speaker: Lu Wang Affiliation: University of Wisconsin–Madison; Member, School of Mathematics Date: January 22, 2019 For more video please visit http://video.ias.edu
From playlist Variational Methods in Geometry
Emanuel Milman - The log-Minkowski Problem - IPAM at UCLA
Recorded 09 February 2022. Emanuel Milman of Technion - Israel Institute of Technology presents "The log-Minkowski Problem" at IPAM's Calculus of Variations in Probability and Geometry Workshop. Abstract: The classical Minkowski problem asks to find a convex body K in Rn having a prescrib
From playlist Workshop: Calculus of Variations in Probability and Geometry

The Maths of General Relativity (5/8) - Curvature
In this series, we build together the theory of general relativity. This fifth video focuses on the notion of curvature, and the different tensors that are used to characterize it. For more videos, subscribe to the YouTube channel : https://www.youtube.com/ScienceClicEN And if you liked t
From playlist The Maths of General Relativity

Marston Morse - An Isoperimetric Concept for the Mass in General Relativity - Gerhard Huisken
Gerhard Huisken Max-Planck Institute for Gravitational Physics March 20, 2009 For more videos, visit http://video.ias.edu
From playlist Mathematics

Recent advances in Geometric Analysis - 4 June 2018
http://crm.sns.it/event/435 The aim of the workshop is to bring together experts working on different sides of Geometric Analysis: PDE aspects, minimal or constant mean curvature surfaces, geometric inequalities, applications to general relativity and others. Financial support for young
From playlist Centro di Ricerca Matematica Ennio De Giorgi

Schwarzian derivatives and Epstein surfaces (Lecture 02) by Ken Bromberg
DISCUSSION MEETING SURFACE GROUP REPRESENTATIONS AND PROJECTIVE STRUCTURES ORGANIZERS: Krishnendu Gongopadhyay, Subhojoy Gupta, Francois Labourie, Mahan Mj and Pranab Sardar DATE: 10 December 2018 to 21 December 2018 VENUE: Ramanujan Lecture Hall, ICTS Bangalore The study of spaces o
From playlist Surface group representations and Projective Structures (2018)

Tensor Calculus Lecture 8e: The Riemann Christoffel Tensor & Gauss's Remarkable Theorem
This course will eventually continue on Patreon at http://bit.ly/PavelPatreon Textbook: http://bit.ly/ITCYTNew Errata: http://bit.ly/ITAErrata McConnell's classic: http://bit.ly/MCTensors Table of Contents of http://bit.ly/ITCYTNew Rules of the Game Coordinate Systems and the Role of Te
From playlist Introduction to Tensor Calculus

IMS Public Lecture: Bubbles-Foams, Grains-Metals: Curvature Flow in Cellular Materials
David J. Srolovitz, University of Pennsylvania, USA and Penn Institute for Computational Science, USA
From playlist Public Lectures

Horizontal Flow of Ideal Fluids | Deriving the Bernoulli Equation
In this video, we will derive the Bernoulli equation. It describes how a liquid flows, for instance through a pipe with varying cross section. But it can also be used to describe the laminar flow of gases at not too high velocities. Contents: 00:00 Overview 00:44 Derivation If you want t
From playlist Classical Mechanics

Daniel Stern - Level set methods for scalar curvature on three-manifolds
We'll discuss a circle of ideas developed over the last few years relating scalar curvature lower bounds to the structure of level sets of solutions to certain geometric pdes on 3-manifolds. We'll describe applications to the study of 3-manifold geometry and initial data sets in general re
From playlist Not Only Scalar Curvature Seminar