
Calculus - The Fundamental Theorem, Part 1
The Fundamental Theorem of Calculus. First video in a short series on the topic. The theorem is stated and two simple examples are worked.
From playlist Calculus - The Fundamental Theorem of Calculus
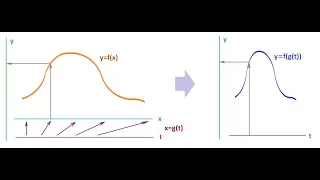
Change of variables and the derivative -- Calculus I
This lecture is on Calculus I. It follows Part I of the book Calculus Illustrated by Peter Saveliev. The text of the book can be found at http://calculus123.com.
From playlist Calculus I

The Fundamental Theorem of Calculus -- Calculus I
This lecture is on Calculus I. It follows Part I of the book Calculus Illustrated by Peter Saveliev. The text of the book can be found at http://calculus123.com.
From playlist Calculus I

The Fundamental Theorem of Calculus | Algebraic Calculus One | Wild Egg
In this video we lay out the Fundamental Theorem of Calculus --from the point of view of the Algebraic Calculus. This key result, presented here for the very first time (!), shows how to generalize the Fundamental Formula of the Calculus which we presented a few videos ago, incorporating t
From playlist Algebraic Calculus One

What is the Fundamental theorem of Algebra, really? | Abstract Algebra Math Foundations 217
Here we give restatements of the Fundamental theorems of Algebra (I) and (II) that we critiqued in our last video, so that they are now at least meaningful and correct statements, at least to the best of our knowledge. The key is to abstain from any prior assumptions about our understandin
From playlist Math Foundations

The Second Fundamental Theorem of Calculus
This video introduces and provides some examples of how to apply the Second Fundamental Theorem of Calculus. Site: http://mathispower4u.com
From playlist The Second Fundamental Theorem of Calculus

This talk is the first of two talks that give a proof of the Riemann Roch theorem, in the spacial case of nonsingular complex plane curves. We divide the Riemann-Roch theorem into 3 pieces: Riemann's theorem, a topological theorem identifying the three definitions of the genus, and Roch'
From playlist Algebraic geometry: extra topics
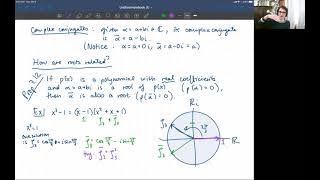
Fundamental Theorem of Algebra
The Fundamental Theorem of Algebra and some additional notes about how roots of polynomials and complex numbers are related to each other.
From playlist Modern Algebra

Entropy of manifolds and of their fundamental group - Gerard Besson
Workshop on Geometric Functionals: Analysis and Applications Topic: Entropy of manifolds and of their fundamental group Speaker: Gerard Besson Affiliation: Université de Grenoble Date: March 7, 2019 For more video please visit http://video.ias.edu
From playlist Mathematics

Calculus 5.3 The Fundamental Theorem of Calculus
My notes are available at http://asherbroberts.com/ (so you can write along with me). Calculus: Early Transcendentals 8th Edition by James Stewart
From playlist Calculus

Dynamics on character varieties - William Goldman
Character Varieties, Dynamics and Arithmetic Topic: Dynamics on character varieties Speaker: William Goldman Affiliation: University of Maryland; Member, School of Mathematics Date: November 10, 2021 In these two talks, I will describe how the classification of locally homogeneous geomet
From playlist Mathematics

16/11/2015 - Jean-Pierre Bourguignon - General Relativity and Geometry
https://philippelefloch.files.wordpress.com/2015/11/2015-ihp-jpbourguignon.pdf Abstract. Physics and Geometry have a long history in common, but the Theory of General Relativity, and theories it triggered, have been a great source of challenges and inspiration for geometers. It started eve
From playlist 2015-T3 - Mathematical general relativity - CEB Trimester

[BOURBAKI 2019] Higher rank Teichmüller theories - Pozzetti - 30/03/19
Beatrice POZZETTI Higher rank Teichmüller theories Let Γ be the fundamental group of a compact surface S with negative Euler characteristic, and G denote PSL(2, R), the group of isometries of the hyperbolic plane. Goldman observed that the Teichmüller space, the parameter space of marked
From playlist BOURBAKI - 2019

Geometry of Surfaces - Topological Surfaces Lecture 1 : Oxford Mathematics 3rd Year Student Lecture
This is the first of four lectures from Dominic Joyce's 3rd Year Geometry of Surfaces course. The four lectures cover topological surfaces and conclude with a big result, namely the classification of surfaces. This lecture provides an introduction to the course and to topological surfaces.
From playlist Oxford Mathematics Student Lectures - Geometry of Surfaces

A. Mondino - Metric measure spaces satisfying Ricci curvature lower bounds 2 (version temporaire)
The idea of compactifying the space of Riemannian manifolds satisfying Ricci curvature lower bounds goes back to Gromov in the '80ies and was pushed by Cheeger-Colding in the ‘90ies, who investigated the structure of spaces arising as Gromov-Hausdorff limits of smooth Riemannian manifolds
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

A. Mondino - Metric measure spaces satisfying Ricci curvature lower bounds 2
The idea of compactifying the space of Riemannian manifolds satisfying Ricci curvature lower bounds goes back to Gromov in the '80ies and was pushed by Cheeger-Colding in the ‘90ies, who investigated the structure of spaces arising as Gromov-Hausdorff limits of smooth Riemannian manifolds
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

Mikhail Gromov - 1/4 Old, New and Unknown around Scalar Curvature
Geometry of scalar curvature, that is comparable in scope to symplectic geometry, mediates between two worlds: the domain of rigidity, one sees in convexity and the realm of softness, characteristic of topology, such as the cobordism theory. The aim of this course is threefold: 1. An ove
From playlist Mikhail Gromov - Old, New and Unknown around Scalar Curvature

Gérard Besson: Some open 3-manifolds
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Algebraic and Complex Geometry

Holomorphic Cartan geometries on simply connected manifolds by Sorin Dumitrescu
Discussion Meeting Complex Algebraic Geometry ORGANIZERS: Indranil Biswas, Mahan Mj and A. J. Parameswaran DATE:01 October 2018 to 06 October 2018 VENUE: Madhava Lecture Hall, ICTS, Bangalore The discussion meeting on Complex Algebraic Geometry will be centered around the "Infosys-ICT
From playlist Complex Algebraic Geometry 2018

Learn to evaluate the integral with functions as bounds
👉 Learn about the fundamental theorem of calculus. The fundamental theorem of calculus is a theorem that connects the concept of differentiation with the concept of integration. The theorem is basically saying that the differentiation of the integral of a function yields the original funct
From playlist Evaluate Using The Second Fundamental Theorem of Calculus