
In this tutorial we define a subgroup and prove two theorem that help us identify a subgroup. These proofs are simple to understand. There are also two examples of subgroups.
From playlist Abstract algebra

Definition of a Subgroup in Abstract Algebra with Examples of Subgroups
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Definition of a Subgroup in Abstract Algebra with Examples of Subgroups
From playlist Abstract Algebra

Abstract Algebra | The notion of a subgroup.
We present the definition of a subgroup and give some examples. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

Abstract Algebra | Normal Subgroups
We give the definition of a normal subgroup and give some examples. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra
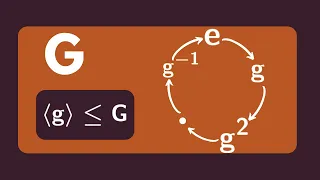
Abstract Algebra | Cyclic Subgroups
We define the notion of a cyclic subgroup and give a few examples. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra
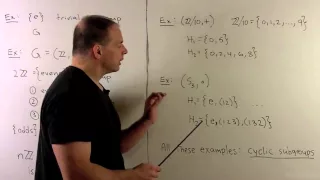
Abstract Algebra: We define the notion of a subgroup and provide various examples. We also consider cyclic subgroups and subgroups generated by subsets in a given group G. Example include A4 and D8. U.Reddit course materials available at http://ureddit.com/class/23794/intro-to-group-
From playlist Abstract Algebra

Abstract Algebra 1.3 : Subgroups, Normal Subgroups, and the Quotient Group
In this video, I introduce subgroups, normal subgroups, and the quotient group generated by a normal subgroup. Email : fematikaqna@gmail.com Code : https://github.com/Fematika/Animations Notes : None yet
From playlist Abstract Algebra

Before we carry on with our coset journey, we need to discover when the left- and right cosets are equal to each other. The obvious situation is when our group is Abelian. The other situation is when the subgroup is a normal subgroup. In this video I show you what a normal subgroup is a
From playlist Abstract algebra

Bettina EICK - Computational group theory, cohomology of groups and topological methods 5
The lecture series will give an introduction to the computer algebra system GAP, focussing on calculations involving cohomology. We will describe the mathematics underlying the algorithms, and how to use them within GAP. Alexander Hulpke's lectures will being with some general computation
From playlist École d'Été 2022 - Cohomology Geometry and Explicit Number Theory

Bettina EICK - Computational group theory, cohomology of groups and topological methods 2
The lecture series will give an introduction to the computer algebra system GAP, focussing on calculations involving cohomology. We will describe the mathematics underlying the algorithms, and how to use them within GAP. Alexander Hulpke's lectures will being with some general computation
From playlist École d'Été 2022 - Cohomology Geometry and Explicit Number Theory

Normal Subgroups and Quotient Groups (aka Factor Groups) - Abstract Algebra
Normal subgroups are a powerful tool for creating factor groups (also called quotient groups). In this video we introduce the concept of a coset, talk about which subgroups are “normal” subgroups, and show when the collection of cosets can be treated as a group of their own. As a motivat
From playlist Abstract Algebra

DATE & TIME 05 November 2016 to 14 November 2016 VENUE Ramanujan Lecture Hall, ICTS Bangalore Computational techniques are of great help in dealing with substantial, otherwise intractable examples, possibly leading to further structural insights and the detection of patterns in many abstra
From playlist Group Theory and Computational Methods

DATE & TIME 05 November 2016 to 14 November 2016 VENUE Ramanujan Lecture Hall, ICTS Bangalore Computational techniques are of great help in dealing with substantial, otherwise intractable examples, possibly leading to further structural insights and the detection of patterns in many abstra
From playlist Group Theory and Computational Methods

TMCF workshop - Enriching latent class models with counterfactual prediction, Mark Gilthorpe
Prediction algorithms in AI use machine learning and statistics to make predictions about an event, given what we know now. Examples include whether a covid-19 patient will require ventilation, or whether a person seeking insurance will make a claim. These predictions can be used for plann
From playlist Theory and Methods Challenge Fortnights

Vincent Guirardel: Natural subgroups of automorphisms
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Algebra

Mazur's program B. - Zureick-Brown - Workshop 2 - CEB T2 2019
David Zureick-Brown (Emory University, Atlanta USA) / 25.06.2019 Mazur's program B. I’ll discuss recent progress on Mazur’s “Program B” – the problem of classifying all possibilities for the “image of Galois” for an elliptic curve over Q (equivalently, classification of all rational poi
From playlist 2019 - T2 - Reinventing rational points

Imprimitive irreducible representations of finite quasisimple groups by Gerhard Hiss
DATE & TIME 05 November 2016 to 14 November 2016 VENUE Ramanujan Lecture Hall, ICTS Bangalore Computational techniques are of great help in dealing with substantial, otherwise intractable examples, possibly leading to further structural insights and the detection of patterns in many abstra
From playlist Group Theory and Computational Methods

Sejong Park: Double Burnside rings and Mackey functors with applications to fusion systems
The lecture was held within the framework of the (Junior) Hausdorff Trimester Program Topology: Workshop "Fusion systems and equivariant algebraic topology"
From playlist HIM Lectures: Junior Trimester Program "Topology"

Why Normal Subgroups are Necessary for Quotient Groups
Proof that cosets are disjoint: https://youtu.be/uxhAUmgSHnI In order for a subgroup to create a quotient group (also known as factor group), it must be a normal subgroup. That means that when we conjugate an element in the subgroup, it stays in the subgroup. In this video, we explain wh
From playlist Group Theory

Stefaan Vaes, Superrigidity for dense subgroups of Lie groups and their actions on homogeneous space
Noncommutative Geometry Seminar (Europe), Oct. 6, 2021
From playlist Global Noncommutative Geometry Seminar (Europe)