
What is a Manifold? Lesson 2: Elementary Definitions
This lesson covers the basic definitions used in topology to describe subsets of topological spaces.
From playlist What is a Manifold?

Manifolds 1.1 : Basic Definitions
In this video, I give the basic intuition and definitions of manifolds. Email : fematikaqna@gmail.com Code : https://github.com/Fematika/Animations Notes : None yet
From playlist Manifolds

What is a Manifold? Lesson 6: Topological Manifolds
Topological manifolds! Finally! I had two false starts with this lesson, but now it is fine, I think.
From playlist What is a Manifold?

Manifolds 1.2 : Examples of Manifolds
In this video, I describe basic examples of manifolds. Email : fematikaqna@gmail.com Code : https://github.com/Fematika/Animations Notes : http://docdro.id/IZO0G25
From playlist Manifolds

What is a Manifold? Lesson 12: Fiber Bundles - Formal Description
This is a long lesson, but it is not full of rigorous proofs, it is just a formal definition. Please let me know where the exposition is unclear. I din't quite get through the idea of the structure group of a fiber bundle fully, but I introduced it. The examples in the next lesson will h
From playlist What is a Manifold?

Manifolds #5: Tangent Space (part 1)
Today, we introduce the notion of tangent vectors and the tangent vector space at a point on a manifold.
From playlist Manifolds

What is a Manifold? Lesson 14: Quotient Spaces
I AM GOING TO REDO THIS VIDEO. I have made some annotations here and annotations are not visible on mobile devices. STAY TUNED. This is a long lesson about an important topological concept: quotient spaces.
From playlist What is a Manifold?

Manifolds 1.4 : Topological Properties
In this video, I introduce the fact that manifolds have a countable basis of precompact coordinate balls, are locally compact, are locally path connected, and are paracompact. Email : fematikaqna@gmail.com Code : https://github.com/Fematika/Animations Notes : None yet Playlist : https://w
From playlist Manifolds

Propagation of Lagrangian States Under random Potentials by Martin Vogel
PROGRAM: TOPICS IN HIGH DIMENSIONAL PROBABILITY ORGANIZERS: Anirban Basak (ICTS-TIFR, India) and Riddhipratim Basu (ICTS-TIFR, India) DATE & TIME: 02 January 2023 to 13 January 2023 VENUE: Ramanujan Lecture Hall This program will focus on several interconnected themes in modern probab
From playlist TOPICS IN HIGH DIMENSIONAL PROBABILITY

A. Song - On the essential minimal volume of Einstein 4-manifolds (version temporaire)
Given a positive epsilon, a closed Einstein 4-manifold admits a natural thick-thin decomposition. I will explain how, for any delta, one can modify the Einstein metric to a bounded sectional curvature metric so that the thick part has volume linearly bounded by the Euler characteristic and
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

A. Song - On the essential minimal volume of Einstein 4-manifolds
Given a positive epsilon, a closed Einstein 4-manifold admits a natural thick-thin decomposition. I will explain how, for any delta, one can modify the Einstein metric to a bounded sectional curvature metric so that the thick part has volume linearly bounded by the Euler characteristic and
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

A. Song - What is the (essential) minimal volume? 4
I will discuss the notion of minimal volume and some of its variants. The minimal volume of a manifold is defined as the infimum of the volume over all metrics with sectional curvature between -1 and 1. Such an invariant is closely related to "collapsing theory", a far reaching set of resu
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

A. Song - What is the (essential) minimal volume? 4 (version temporaire)
I will discuss the notion of minimal volume and some of its variants. The minimal volume of a manifold is defined as the infimum of the volume over all metrics with sectional curvature between -1 and 1. Such an invariant is closely related to "collapsing theory", a far reaching set of resu
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

D. Prandri - Weyl law for singular Riemannian manifolds
In this talk we present recent results on the asymptotic growth of eigenvalues of the Laplace-Beltrami operator on singular Riemannian manifolds, where all geometrical invariants appearing in classical spectral asymptotics are unbounded, and the total volume can be infinite. Under suitable
From playlist Journées Sous-Riemanniennes 2018

A. Song - What is the (essential) minimal volume? 3
I will discuss the notion of minimal volume and some of its variants. The minimal volume of a manifold is defined as the infimum of the volume over all metrics with sectional curvature between -1 and 1. Such an invariant is closely related to "collapsing theory", a far reaching set of resu
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

Minimality and stable ergodicity by Jana Rodriguez Hertz
PROGRAM SMOOTH AND HOMOGENEOUS DYNAMICS ORGANIZERS: Anish Ghosh, Stefano Luzzatto and Marcelo Viana DATE: 23 September 2019 to 04 October 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Ergodic theory has its origins in the the work of L. Boltzmann on the kinetic theory of gases.
From playlist Smooth And Homogeneous Dynamics

A. Song - What is the (essential) minimal volume? 3 (version temporaire)
I will discuss the notion of minimal volume and some of its variants. The minimal volume of a manifold is defined as the infimum of the volume over all metrics with sectional curvature between -1 and 1. Such an invariant is closely related to "collapsing theory", a far reaching set of resu
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics
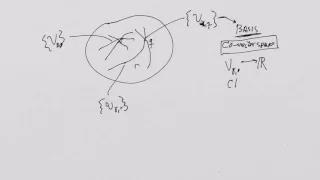
What is a Manifold? Lesson 10: Tangent Space - Basis Vectors
What is a Manifold? Lesson 10: Tangent Space - Basis Vectors
From playlist What is a Manifold?

Simone Cecchini: A long neck principle for Riemannian spin manifolds with positive scalar curvature
Talk by Jonathan Rosenberg in Global Noncommutative Geometry Seminar (Americas) http://www.math.wustl.edu/~xtang/NCG-Seminar.html on September 30, 2020.
From playlist Global Noncommutative Geometry Seminar (Americas)
