Quadrics | Surfaces | Geometric shapes
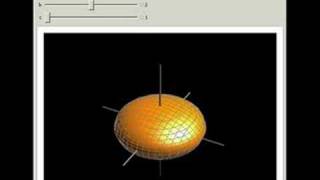
Ellipsoid
An ellipsoid is a surface that may be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation. An ellipsoid is a quadric surface; that is, a surface that may be defined as the zero set of a polynomial of degree two in three variables. Among quadric surfaces, an ellipsoid is characterized by either of the two following properties. Every planar cross section is either an ellipse, or is empty, or is reduced to a single point (this explains the name, meaning "ellipse-like"). It is bounded, which means that it may be enclosed in a sufficiently large sphere. An ellipsoid has three pairwise perpendicular axes of symmetry which intersect at a center of symmetry, called the center of the ellipsoid. The line segments that are delimited on the axes of symmetry by the ellipsoid are called the principal axes, or simply axes of the ellipsoid. If the three axes have different lengths, the figure is a triaxial ellipsoid (rarely scalene ellipsoid), and the axes are uniquely defined. If two of the axes have the same length, then the ellipsoid is an ellipsoid of revolution, also called a spheroid. In this case, the ellipsoid is invariant under a rotation around the third axis, and there are thus infinitely many ways of choosing the two perpendicular axes of the same length. If the third axis is shorter, the ellipsoid is an oblate spheroid; if it is longer, it is a prolate spheroid. If the three axes have the same length, the ellipsoid is a sphere. (Wikipedia).