
Topology (What is a Topology?)
What is a Topology? Here is an introduction to one of the main areas in mathematics - Topology. #topology Some of the links below are affiliate links. As an Amazon Associate I earn from qualifying purchases. If you purchase through these links, it won't cost you any additional cash, b
From playlist Topology

Lower Bound on Complexity - Intro to Algorithms
This video is part of an online course, Intro to Algorithms. Check out the course here: https://www.udacity.com/course/cs215.
From playlist Introduction to Algorithms

The Computational Complexity of Geometric Topology Problems - Greg Kuperberg
Greg Kuperberg University of California, Davis September 24, 2012 This talk will be a partial survey of the first questions in the complexity theory of geometric topology problems. What is the complexity, or what are known complexity bounds, for distinguishing n-manifolds for various n? Fo
From playlist Mathematics

Algebraic topology: Introduction
This lecture is part of an online course on algebraic topology. This is an introductory lecture, where we give a quick overview of some of the invariants of algebraic topology (homotopy groups, homology groups, K theory, and cobordism). The book "algebraic topology" by Allen Hatcher men
From playlist Algebraic topology

I define closed sets, an important notion in topology and analysis. It is defined in terms of limit points, and has a priori nothing to do with open sets. Yet I show the important result that a set is closed if and only if its complement is open. More topology videos can be found on my pla
From playlist Topology

What Is Network Topology? | Types of Network Topology | BUS, RING, STAR, TREE, MESH | Simplilearn
In this video on Network Topology, we will understand What is Network topology, the role of using topology while designing a network, Different types of Topologies in a Network. Network topology provides us with a way to configure the most optimum network design according to our requiremen
From playlist Cyber Security Playlist [2023 Updated]🔥

Algebraic Topology - 5.1 - Mappings Spaces and the Compact Open Topology
We define the compact open topology on mapping spaces.
From playlist Algebraic Topology

Topology 1.7 : More Examples of Topologies
In this video, I introduce important examples of topologies I didn't get the chance to get to. This includes The discrete and trivial topologies, subspace topology, the lower-bound and K topologies on the reals, the dictionary order, and the line with two origins. I also introduce (again)
From playlist Topology

Topology 1.1 : Open Sets of Reals
In this video, I give a definition of the open sets on the real numbers. Email : fematikaqna@gmail.com Code : https://github.com/Fematika/Animations Notes : None yet
From playlist Topology

Teena Gerhardt - 1/3 Algebraic K-theory and Trace Methods
Algebraic K-theory is an invariant of rings and ring spectra which illustrates a fascinating interplay between algebra and topology. Defined using topological tools, this invariant has important applications to algebraic geometry, number theory, and geometric topology. One fruitful approac
From playlist Summer School 2020: Motivic, Equivariant and Non-commutative Homotopy Theory

Elchanan Solomon (08/25/21): Dimensionality Reduction via Distributed Persistence: DIPOLE
Title: Dimensionality Reduction via Distributed Persistence: DIPOLE Abstract: We propose a new gradient-descent-based paradigm for dimensionality reduction, called DIPOLE, consisting of a loss function with two terms: a local metric term that forces the projection to be an isometry on sm
From playlist AATRN 2021

Elba Garcia-Failde: Introduction to topological recursion - Lecture 1
Mini course of the conference "Noncommutative geometry meets topological recursion", August 2021, University of Münster. Abstract: In this mini-course I will introduce the universal procedure of topological recursion, both by treating examples and by presenting the general formalism. We wi
From playlist Noncommutative geometry meets topological recursion 2021

Quantum Topological Data Analysis (Part 1) [Péguy Kem-Meka]
Quantum Topological Data Analysis is about how quantum computers and quantum information processors can learn pattern in data that cannot be learn by classical TDA algorithms. Quantum computers are becoming available to general public. They can dramatically reduce both execution time and e
From playlist Tutorials

Xie Chen - CS+Physics - Alumni College 2016
"Topological Quantum Computation" Xie Chen, Assistant Professor of Theoretical Physics, is a condensed-matter theorist who examines quantum-mechanical systems with a large number of degrees of freedom. She is interested in learning how the constituent degrees of freedom cooperate with one
From playlist Talks and Seminars
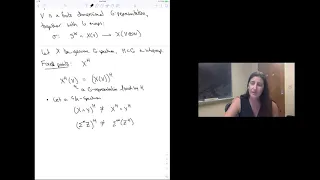
Teena Gerhardt - 2/3 Algebraic K-theory and Trace Methods
Algebraic K-theory is an invariant of rings and ring spectra which illustrates a fascinating interplay between algebra and topology. Defined using topological tools, this invariant has important applications to algebraic geometry, number theory, and geometric topology. One fruitful approac
From playlist Summer School 2020: Motivic, Equivariant and Non-commutative Homotopy Theory

Topologically Ordered Matter and Why You Should be Interested by Steven H. Simon
COLLOQUIUM TOPOLOGICALLY ORDERED MATTER AND WHY YOU SHOULD BE INTERESTED SPEAKER: Steven H. Simon (Oxford University, United Kingdom) DATE: Mon, 26 October 2020, 15:30 to 17:00 VENUE: Online ABSTRACT In two dimensional topologically ordered matter, processes depend on gross topology
From playlist ICTS Colloquia

Exploring state-space topology in the geosciences - Sciamarella - Workshop 1 - CEB T3 2019
Sciamarella (CNRS) / 11.10.2019 Exploring state-space topology in the geosciences ************************************* Langue : Anglais ; Date : 11.10.2019; Conférencier : Sciamarella, Denisse; Évenement : Workshop 1 - CEB T3 2019; Lieu : IHP; Mots Clés :
From playlist 2019 - T3 - The Mathematics of Climate and the Environment

An introduction to homology (cont.) | Algebraic Topology | NJ Wildberger
Here we carry on our introduction to homology, focussing on a particularly simple space, basically a graph and various modifications to it. We discuss cycles, boundaries, and homology as a quotient of cycles mod boundaries, one such group for each dimension. The framework is commutative g
From playlist Algebraic Topology

Teena Gerhardt - 3/3 Algebraic K-theory and Trace Methods
Algebraic K-theory is an invariant of rings and ring spectra which illustrates a fascinating interplay between algebra and topology. Defined using topological tools, this invariant has important applications to algebraic geometry, number theory, and geometric topology. One fruitful approac
From playlist Summer School 2020: Motivic, Equivariant and Non-commutative Homotopy Theory
