
Function Comparision - Intro to Algorithms
This video is part of an online course, Intro to Algorithms. Check out the course here: https://www.udacity.com/course/cs215.
From playlist Introduction to Algorithms

Describing Functions (Discrete Math)
This video covered the various ways to describe functions in a discrete math class.
From playlist Functions (Discrete Math)

Functions of equations - IS IT A FUNCTION
👉 Learn how to determine whether relations such as equations, graphs, ordered pairs, mapping and tables represent a function. A function is defined as a rule which assigns an input to a unique output. Hence, one major requirement of a function is that the function yields one and only one r
From playlist What is the Domain and Range of the Function

Determine if a Relation is a Function
http://mathispower4u.wordpress.com/
From playlist Intro to Functions

Theory of numbers: Multiplicative functions
This lecture is part of an online undergraduate course on the theory of numbers. Multiplicative functions are functions such that f(mn)=f(m)f(n) whenever m and n are coprime. We discuss some examples, such as the number of divisors, the sum of the divisors, and Euler's totient function.
From playlist Theory of numbers
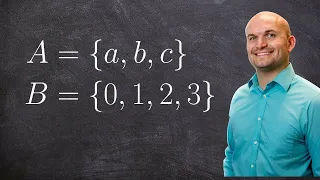
How to determine if an ordered pair is a function or not
👉 Learn how to determine whether relations such as equations, graphs, ordered pairs, mapping and tables represent a function. A function is defined as a rule which assigns an input to a unique output. Hence, one major requirement of a function is that the function yields one and only one r
From playlist What is the Domain and Range of the Function

How to determine if a set of points is a function, onto, one to one, domain, range
👉 Learn how to determine whether relations such as equations, graphs, ordered pairs, mapping and tables represent a function. A function is defined as a rule which assigns an input to a unique output. Hence, one major requirement of a function is that the function yields one and only one r
From playlist What is the Domain and Range of the Function

What is an Injective Function? Definition and Explanation
An explanation to help understand what it means for a function to be injective, also known as one-to-one. The definition of an injection leads us to some important properties of injective functions! Subscribe to see more new math videos! Music: OcularNebula - The Lopez
From playlist Functions
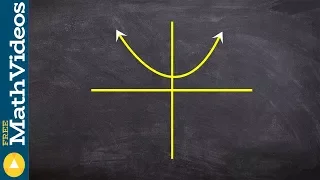
Using the vertical line test to determine if a graph is a function or not
👉 Learn how to determine whether relations such as equations, graphs, ordered pairs, mapping and tables represent a function. A function is defined as a rule which assigns an input to a unique output. Hence, one major requirement of a function is that the function yields one and only one r
From playlist What is the Domain and Range of the Function

Failure of the computable weak Kőnig's lemma
Constructing a decidable binary tree with infinitely many vertices that does not have a computable infinite path. In analysis contexts such as RCA0 or CZF, the non-constructive WKL is more or less as strong as Brouwer's fixed point theorem or restricted forms of Brouwer's fan theorem. Text
From playlist Programming

Approximation of generalized ridge functions in high dimensions – Sandra Keiper
Many problems in science and engineering involve an underlying unknown complex process that depends on a large number of parameters. The goal in many applications is to reconstruct, or learn, the unknown process given some direct or indirect observations. Mathematically, such a problem can
From playlist Approximating high dimensional functions

A (truly) universal polynomial differential equation Lee A. Rubel proved in 1981 that there exists a universal fourth-order algebraic differential equation P(y,y',y'',y''')=0 (1) and provided an explicit example. It is universal in the sense that for any continuous function f from R to
From playlist DART X

Andrew Sutherland, Arithmetic L-functions and their Sato-Tate distributions
VaNTAGe seminar on April 28, 2020. License: CC-BY-NC-SA Closed captions provided by Jun Bo Lau.
From playlist The Sato-Tate conjecture for abelian varieties

From playlist Atelier PARI/GP 2016

Alain Connes - Prolate Wave Operator and Zeta
This is joint work with Henri Moscovici in which we show that the ultraviolet spectrum of the selfadjoint extension of the prolate wave operator matches the squares of the zeros of the Riemann zeta function. Alain Connes (IHES, Collège de France)
From playlist Mikefest: A conference in honor of Michael Douglas' 60th birthday

Function Singularities and Their Applications
For the latest information, please visit: http://www.wolfram.com Speaker: Adam Strzebonski Wolfram developers and colleagues discussed the latest in innovative technologies for cloud computing, interactive deployment, mobile devices, and more.
From playlist Wolfram Technology Conference 2016

A look at how to write integration and unit tests in Rust, including how to mock dependencies so that parts of the system can be tested in isolation. 00:00 Intro 00:53 Integration Tests 02:57 Unit Tests 04:17 Assert Macros 04:52 should_panic and ignored 05:43 cargo test 07:10 Mocking 11:5
From playlist Great Rust Videos

Computing Principal Eigenvalue in Interval Arithmetic
Jiri Benedikt
From playlist Wolfram Technology Conference 2019

Computably enumerable sets and undecidability
In this video we're going to define and implement decidable as well as semidecidable. Code is found under https://gist.github.com/Nikolaj-K/808149debf7c3b09705127f9205f6c3f Other names for the two are recursive or computable resp. recursively enumerable, computably enumerable - I also say
From playlist Programming

Represent a Discrete Function Using Ordered Pairs, a Table, and Function Notation
This video explains how to represent a discrete function given as points as ordered pairs, a table, and using function notation. http://mathispower4u.com
From playlist Introduction to Functions: Function Basics