The Meaning of Numbers – Categorical Data (1-2)
Numbers can do many functions. Some numbers stand in for names or create categories (nominal & ordinal). Other numbers quantify amounts and measurements (interval & ratio). We begin with categorical data: nominal and ordinal. You will learn the distinctions between nominal and ordinal data
From playlist WK1 Numbers and Variables - Online Statistics for the Flipped Classroom

From playlist Thinking about Data

R Programming: Introduction: Factors (R Intro-04)
[my R script is here https://github.com/bionicturtle/youtube/tree/master/r-intro] Factors are categorical vectors. Specifically, they are (integer) vectors that store categorical values, or ordinal values. Ordinal values are *ranked* categories (but they are not intervals).Factors can only
From playlist R Programming: Intro

Math 060 Fall 2017 111317C Orthonormal Bases
Motivation: how to obtain the coordinate vector with respect to a given basis? Definition: orthogonal set. Example. Orthogonal implies linearly independent. Orthonormal sets. Example of an orthonormal set. Definition: orthonormal basis. Properties of orthonormal bases. Example: Fou
From playlist Course 4: Linear Algebra (Fall 2017)
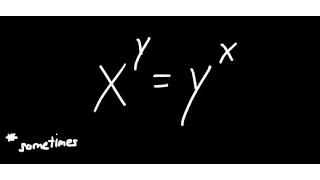
When Does Exponentiation Commute? (Part 1)
In this video, I'll show how one can find pairs of numbers that can be commuted under exponentiation. That is, we can find pairs of numbers such that x^y = y^x. We will take this equation, x^y = y^x and parametrize it to find these (x,y) pairs. It turns out that there are infinitely many n
From playlist Math

Orthogonal and Orthonormal Sets of Vectors
This video defines orthogonal and orthonormal sets of vectors.
From playlist Orthogonal and Orthonormal Sets of Vectors

Function Comparision - Intro to Algorithms
This video is part of an online course, Intro to Algorithms. Check out the course here: https://www.udacity.com/course/cs215.
From playlist Introduction to Algorithms

Orthonormal bases. The Gram-Schmidt Procedure. Schuur's Theorem on upper-triangular matrix with respect to an orthonormal basis. The Riesz Representation Theorem.
From playlist Linear Algebra Done Right

Infinite Sets and Foundations (Joel David Hamkins) | Ep. 17
Joel David Hamkins is a Professor of Logic with appointments in Philosophy and Mathematics at Oxford University. His main interest is in set theory. We discuss the field of set theory: what it can say about infinite sets and which issues are unresolved, and the relation of set theory to ph
From playlist Daniel Rubin Show, Full episodes

A conversation between Gregory Chaitin and Stephen Wolfram, Part 2
Stephen Wolfram plays the role of Salonnière in this new, on-going series of intellectual explorations with special guests. Watch all of the conversations here: https://wolfr.am/youtube-sw-conversations Originally livestreamed at: https://twitch.tv/stephen_wolfram Stay up-to-date on
From playlist Conversations with Special Guests

Rick Sommer - Knuth’s Up-Arrow into the Transfinite & Beyond! - G4G14 Apr 2022
Famous for its world-record status, Graham’s number has captured the imagination of recreational mathematicians ever since being introduced by Martin Gardner in Mathematical Recreations in 1977. Knuth’s up-arrow notation builds on a nifty recursion that is used to define Graham’s number, a
From playlist G4G14 Videos

Live CEOing Ep 531: Language Design in Wolfram Language [Strings & Numbers, WFR Submissions & More]
In this episode of Live CEOing, Stephen Wolfram discusses upcoming improvements and features to the Wolfram Language. If you'd like to contribute to the discussion in future episodes, you can participate through this YouTube channel or through the official Twitch channel of Stephen Wolfram
From playlist Behind the Scenes in Real-Life Software Design

Ordinals of countable order type beyond infinity
We implement an order of order type beyond the first infinite one, in a straight forward fashion. To that end, we arrange the natural numbers in an order with countably infinitely many jumps. So there are many numbers that come, with respect to our order, after an infinite amount of number
From playlist Programming

Axioms of Constructive Set Theory Explained
In this video we're going to discuss the various axiom schemes of constructive set theories and how they relate to type theory. I cover BCST, ECST, IKP, KPI, KP, CST, CZF, IZF, Mac Lane, Z and variants equi-consistent to ETCS from category theory, and then of course ZF and ZFC. The text I
From playlist Logic

Kill the Mathematical Hydra | Infinite Series
Viewers like you help make PBS (Thank you 😃) . Support your local PBS Member Station here: https://to.pbs.org/donateinfi How do you defeat a creature that grows two heads for every one head you chop off? You do the math. Thanks to The Great Courses Plus for sponsoring this episode of Infi
From playlist An Infinite Playlist

Linear Algebra - Lecture 39 - Orthonormal Sets
In this lecture, we discuss orthonormal sets of vectors. We investigate matrices with orthonormal columns. We also define an orthogonal matrix.
From playlist Linear Algebra Lectures