Rotational symmetry | Circles | Spherical curves
Circle of a sphere
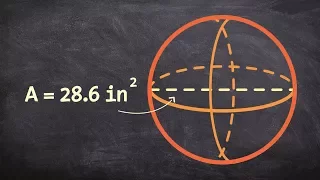
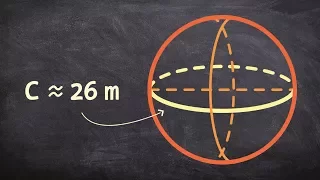
A circle of a sphere is a circle that lies on a sphere. Such a circle can be formed as the intersection of a sphere and a plane, or of two spheres. Circles of a sphere are the spherical geometry analogs of generalised circles in Euclidean space. A circle on a sphere whose plane passes through the center of the sphere is called a great circle, analogous to a Euclidean straight line; otherwise it is a small circle, analogous to a Euclidean circle. Circles of a sphere have radius less than or equal to the sphere radius, with equality when the circle is a great circle. A circle of a sphere can also be characterized as the locus of points on the sphere at uniform distance from a given center point, or as a spherical curve of constant curvature. (Wikipedia).