
This video is about topological spaces and some of their basic properties.
From playlist Basics: Topology

Definition of a Topological Space
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Definition of a Topological Space
From playlist Topology

Introduction to Metric Spaces - Definition of a Metric. - The metric on R - The Euclidean Metric on R^n - A metric on the set of all bounded functions - The discrete metric
From playlist Topology

Topological Spaces: Introduction & Axioms
The first video in a new series on topological spaces and manifolds.
From playlist Topology & Manifolds

This video is about metric spaces and some of their basic properties.
From playlist Basics: Topology

Metric space definition and examples. Welcome to the beautiful world of topology and analysis! In this video, I present the important concept of a metric space, and give 10 examples. The idea of a metric space is to generalize the concept of absolute values and distances to sets more gener
From playlist Topology

Hausdorff Example 3: Function Spaces
Point Set Topology: For a third example, we consider function spaces. We begin with the space of continuous functions on [0,1]. As a metric space, this example is Hausdorff, but not complete. We consider Cauchy sequences and a possible completion.
From playlist Point Set Topology
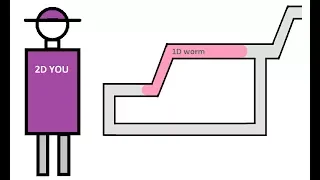
This lecture is on Introduction to Higher Mathematics (Proofs). For more see http://calculus123.com.
From playlist Proofs
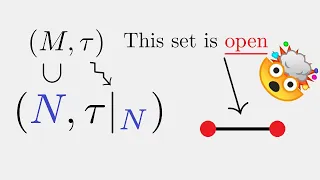
Topological Spaces: The Subspace Topology
Today, we discuss the subspace topology, which is a useful tool to construct new topologies.
From playlist Topology & Manifolds

Lecture 7: Sheaves of sets (Part 2)
The most important examples of topoi are categories of sheaves of sets on a small category. Patrick Eilliott introduced this class of examples over two talks, of which is the second. In this talk he defines Grothendieck topologies and the category of sheaves on a site, and develops the exa
From playlist Topos theory seminar

Clark Barwick - 3/3 Exodromy for ℓ-adic Sheaves
In joint work with Saul Glasman and Peter Haine, we proved that the derived ∞-category of constructible ℓ-adic sheaves ’is’ the ∞-category of continuous functors from an explicitly defined 1-category to the ∞-category of perfect complexes over ℚℓ. In this series of talks, I want to offer s
From playlist Summer School 2020: Motivic, Equivariant and Non-commutative Homotopy Theory

Laurent Lafforgue - 1/4 Classifying toposes of geometric theories
Course at the school and conference “Toposes online” (24-30 June 2021): https://aroundtoposes.com/toposesonline/ Slides: https://aroundtoposes.com/wp-content/uploads/2021/07/LafforgueSlidesToposesOnline.pdf The purpose of these lectures will be to present the theory of classifying topose
From playlist Toposes online

Clark Barwick - 2/3 Exodromy for ℓ-adic Sheaves
In joint work with Saul Glasman and Peter Haine, we proved that the derived ∞-category of constructible ℓ-adic sheaves ’is’ the ∞-category of continuous functors from an explicitly defined 1-category to the ∞-category of perfect complexes over ℚℓ. In this series of talks, I want to offer s
From playlist Summer School 2020: Motivic, Equivariant and Non-commutative Homotopy Theory

Introduction to Homotopy Theory- PART 1: UNIVERSAL CONSTRUCTIONS
The goal of this series is to develop homotopy theory from a categorical perspective, alongside the theory of model categories. We do this with the hope of eventually developing stable homotopy theory, a personal goal a passion of mine. I'm going to follow nLab's notes, but I hope to add t
From playlist Introduction to Homotopy Theory
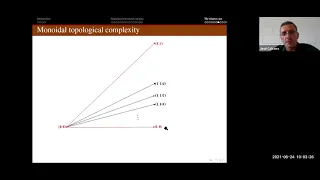
José Manuel García-Calcines (6/24/21): Topological complexity using arbitrary covers
Title: Topological complexity using arbitrary covers
From playlist Topological Complexity Seminar

The rising sea: Grothendieck on simplicity and generality - Colin McLarty [2003]
Slides for this talk: https://drive.google.com/file/d/1yDmqhdcKo6-YpDpRdHh2hvuNirZVbcKr/view?usp=sharing Notes for this talk: https://drive.google.com/open?id=1p45B3Hh8WPRhdhQAd0Wq0MvmY0JYSnmc The History of Algebra in the Nineteenth and Twentieth Centuries April 21 - 25, 2003 Colin Mc
From playlist Mathematics

Nonetheless one should learn the language of topos: Grothendieck... - Colin McLarty [2018]
Grothendieck's 1973 topos lectures Colin McLarty 3 mai 2018 In the summer of 1973 Grothendieck lectured on several subjects in Buffalo NY, and these lectures were recorded, including 33 hours on topos theory. The topos lectures were by far the most informal of the series, with the most si
From playlist Number Theory

Jezus Gonzalez (6/25/17) Bedlewo: Topological complexity and the motion planning problem in robotics
Early this century Michael Farber introduced the concept of Topological Complexity (TC), a model to study the continuity instabilities in the motion planning problem in robotics. Farber’s model has captured much attention since then due to the rich algebraic topology properties encoded by
From playlist Applied Topology in Będlewo 2017
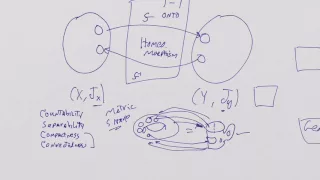
What is a Manifold? Lesson 5: Compactness, Connectedness, and Topological Properties
The last lesson covering the topological prep-work required before we begin the discussion of manifolds. Topics covered: compactness, connectedness, and the relationship between homeomorphisms and topological properties.
From playlist What is a Manifold?
Étale cohomology lecture 3, August 27, 2020
Sites and sheaves, the étale and fppf site, representable functors
From playlist Étale cohomology and the Weil conjectures