
Now that we know what a quotient group is, let's take a look at an example to cement our understanding of the concepts involved.
From playlist Abstract algebra

PreCalculus | Finding the difference quotient: Example 3
We present a few examples of calculating the difference quotient. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist PreCalculus

The idea of a quotient group follows easily from cosets and Lagrange's theorem. In this video, we start with a normal subgroup and develop the idea of a quotient group, by viewing each coset (together with the normal subgroup) as individual mathematical objects in a set. This set, under
From playlist Abstract algebra

Visual Group Theory, Lecture 3.5: Quotient groups
Visual Group Theory, Lecture 3.5: Quotient groups Like how a direct product can be thought of as a way to "multiply" two groups, a quotient is a way to "divide" a group by one of its subgroups. We start by defining this in terms of collapsing Cayley diagrams, until we get a conjecture abo
From playlist Visual Group Theory
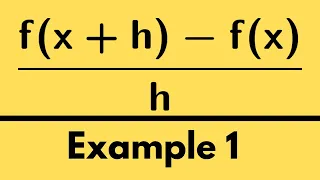
PreCalculus | Find the difference quotient: Example 1
We present a few examples calculating the difference quotient of a function. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist PreCalculus

On finite dimensional omega-categorical structures (...) - P. Simon - Workshop 1 - CEB T1 2018
Pierre Simon (Berkeley) / 31.01.2018 On finite dimensional omega-categorical structures and NIP theories The study of omega-categorical structures lies at the intersection of model theory, combinatorics and group theory. Some classes of omega-categorical structures have been classified,
From playlist 2018 - T1 - Model Theory, Combinatorics and Valued fields

Simplify a rational expression by using properties of exponents
👉 Learn how to simplify expressions using the quotient rule of exponents. The quotient rule of exponents states that the quotient of powers with a common base is equivalent to the power with the common base and an exponent which is the difference of the exponents of the term in the numerat
From playlist Simplify Using the Rules of Exponents | Quotient Rule

Quiver moduli and applications, Markus Reineke (Bochum), Lecture 3
Quiver moduli spaces are algebraic varieties encoding the continuous parameters of linear algebra type classification problems. In recent years their topological and geometric properties have been explored, and applications to, among others, Donaldson-Thomas and Gromov-Witten theory have
From playlist Felix Klein Lectures 2020: Quiver moduli and applications, Markus Reineke (Bochum)

Applying the quotient rule to simplify a rational expression
👉 Learn how to simplify expressions using the quotient rule and the negative exponent rule of exponents. The quotient rule of exponents states that the quotient of powers with a common base is equivalent to the power with the common base and an exponent which is the difference of the expon
From playlist Simplify Using the Rules of Exponents
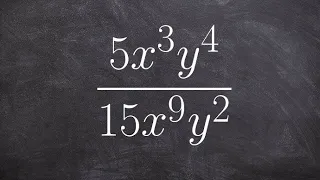
Simplify rational expression using the rules of exponents
👉 Learn how to simplify expressions using the quotient rule of exponents. The quotient rule of exponents states that the quotient of powers with a common base is equivalent to the power with the common base and an exponent which is the difference of the exponents of the term in the numerat
From playlist Simplify Using the Rules of Exponents | Quotient Rule

Peng Shan: Coherent categorification of quantum loop sl(2)
'Coherent categorification of quantum loop sl(2)' Peng Shan (Tsinghua University) Abstract: We explain an equivalence of categories between a module category of quiver Hecke algebras associated with the Kronecker quiver and a category of equivariant perverse coherent sheaves on the nilpot
From playlist SMRI Algebra and Geometry Online

Gromov-Witten Theory and Gauge Theory (Lecture 2) by Constantin Teleman
PROGRAM: VORTEX MODULI ORGANIZERS: Nuno Romão (University of Augsburg, Germany) and Sushmita Venugopalan (IMSc, India) DATE & TIME: 06 February 2023 to 17 February 2023 VENUE: Ramanujan Lecture Hall, ICTS Bengaluru For a long time, the vortex equations and their associated self-dual fie
From playlist Vortex Moduli - 2023

Galois theory: Transcendental extensions
This lecture is part of an online graduate course on Galois theory. We describe transcendental extension of fields and transcendence bases. As applications we classify algebraically closed fields and show hw to define the dimension of an algebraic variety.
From playlist Galois theory

The affine Hecke category is a monoidal colimit - James Tao
Geometric and Modular Representation Theory Seminar Topic: The affine Hecke category is a monoidal colimit Speaker: James Tao Affiliation: Massachusetts Institute of Technology Date: February 24, 2021 For more video please visit http://video.ias.edu
From playlist Seminar on Geometric and Modular Representation Theory

Geordie Williamson: Langlands and Bezrukavnikov II Lecture 14
SMRI Seminar Series: 'Langlands correspondence and Bezrukavnikov’s equivalence' Geordie Williamson (University of Sydney) Abstract: The second part of the course focuses on affine Hecke algebras and their categorifications. Last year I discussed the local Langlands correspondence in bro
From playlist Geordie Williamson: Langlands correspondence and Bezrukavnikov’s equivalence
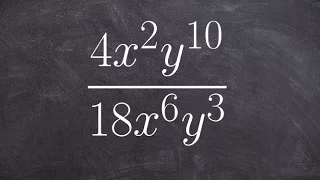
Simplify an expression by applying quotient rule of exponents
👉 Learn how to simplify expressions using the quotient rule of exponents. The quotient rule of exponents states that the quotient of powers with a common base is equivalent to the power with the common base and an exponent which is the difference of the exponents of the term in the numerat
From playlist Simplify Using the Rules of Exponents | Quotient Rule

Ralph KAUFMANN - Categorical Interactions in Algebra, Geometry and Physics
Categorical Interactions in Algebra, Geometry and Physics: Cubical Structures and Truncations There are several interactions between algebra and geometry coming from polytopic complexes as for instance demonstrated by several versions of Deligne's conjecture. These are related through bl
From playlist Algebraic Structures in Perturbative Quantum Field Theory: a conference in honour of Dirk Kreimer's 60th birthday

Learn the basics for simplifying an expression using the rules of exponents
👉 Learn how to simplify expressions using the quotient rule of exponents. The quotient rule of exponents states that the quotient of powers with a common base is equivalent to the power with the common base and an exponent which is the difference of the exponents of the term in the numerat
From playlist Simplify Using the Rules of Exponents | Quotient Rule

