
Now that we know what a quotient group is, let's take a look at an example to cement our understanding of the concepts involved.
From playlist Abstract algebra

Visual Group Theory, Lecture 3.5: Quotient groups
Visual Group Theory, Lecture 3.5: Quotient groups Like how a direct product can be thought of as a way to "multiply" two groups, a quotient is a way to "divide" a group by one of its subgroups. We start by defining this in terms of collapsing Cayley diagrams, until we get a conjecture abo
From playlist Visual Group Theory

PreCalculus | Finding the difference quotient: Example 3
We present a few examples of calculating the difference quotient. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist PreCalculus

The idea of a quotient group follows easily from cosets and Lagrange's theorem. In this video, we start with a normal subgroup and develop the idea of a quotient group, by viewing each coset (together with the normal subgroup) as individual mathematical objects in a set. This set, under
From playlist Abstract algebra
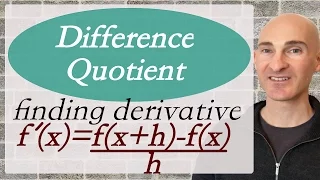
Difference Quotient - What is it? (PreCalculus)
How to find the Difference Quotient. We discuss how the difference quotient represents a formula for the slope between points but as the distance between the two points decreases you get the instant rate of change or the slope of the tangent line. 0:04 What is the Difference Quotient 0:11
From playlist Difference Quotient & Derivatives

Learn the basics for simplifying an expression using the rules of exponents
👉 Learn how to simplify expressions using the quotient rule of exponents. The quotient rule of exponents states that the quotient of powers with a common base is equivalent to the power with the common base and an exponent which is the difference of the exponents of the term in the numerat
From playlist Simplify Using the Rules of Exponents | Quotient Rule
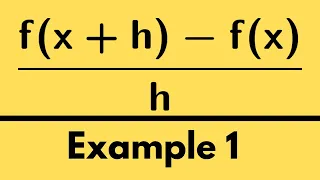
PreCalculus | Find the difference quotient: Example 1
We present a few examples calculating the difference quotient of a function. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist PreCalculus
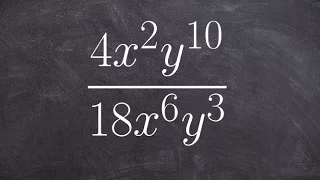
Simplify an expression by applying quotient rule of exponents
👉 Learn how to simplify expressions using the quotient rule of exponents. The quotient rule of exponents states that the quotient of powers with a common base is equivalent to the power with the common base and an exponent which is the difference of the exponents of the term in the numerat
From playlist Simplify Using the Rules of Exponents | Quotient Rule

Cohomological Field Theories from GLSMs (Lecture 1) by David Favero
PROGRAM: VORTEX MODULI ORGANIZERS: Nuno Romão (University of Augsburg, Germany) and Sushmita Venugopalan (IMSc, India) DATE & TIME: 06 February 2023 to 17 February 2023 VENUE: Ramanujan Lecture Hall, ICTS Bengaluru For a long time, the vortex equations and their associated self-dual fie
From playlist Vortex Moduli - 2023

David Rydh. Local structure of algebraic stacks and applications
Abstract: Some natural moduli problems, such as moduli of sheaves and moduli of singular curves, give rise to stacks with infinite stabilizers that are not known to be quotient stacks. The local structure theorem states that many stacks locally look like the quotient of a scheme by the act
From playlist CORONA GS

Variation of FLTZ skeleta - Jesse Huang
Joint IAS/Princeton/Montreal/Paris/Tel-Aviv Symplectic Geometry Topic: Variation of FLTZ skeleta Speaker: Jesse Huang Affiliation: UIUC Date: March 26, 2021 Speaker's corrections: 1) The linear map on page 10 should be sending the basis to 1 and -1, not 1 and 2; 2) one more typo on the
From playlist Mathematics

Cohomological Field Theories from GLSMs (Lecture 2) by David Favero
PROGRAM: VORTEX MODULI ORGANIZERS: Nuno Romão (University of Augsburg, Germany) and Sushmita Venugopalan (IMSc, India) DATE & TIME: 06 February 2023 to 17 February 2023 VENUE: Ramanujan Lecture Hall, ICTS Bengaluru For a long time, the vortex equations and their associated self-dual fie
From playlist Vortex Moduli - 2023

What is a difference quotient? How to find a difference quotient. Deriving it from the rise over run formula.
From playlist Calculus

Emily Cliff: Hilbert Schemes Lecture 6
SMRI Seminar Series: 'Hilbert Schemes' Lecture 6 GIT stability, quiver representations, & Hilbert schemes Emily Cliff (University of Sydney) This series of lectures aims to present parts of Nakajima’s book `Lectures on Hilbert schemes of points on surfaces’ in a way that is accessible to
From playlist SMRI Course: Hilbert Schemes

Quiver moduli and applications, Markus Reineke (Bochum), Lecture 3
Quiver moduli spaces are algebraic varieties encoding the continuous parameters of linear algebra type classification problems. In recent years their topological and geometric properties have been explored, and applications to, among others, Donaldson-Thomas and Gromov-Witten theory have
From playlist Felix Klein Lectures 2020: Quiver moduli and applications, Markus Reineke (Bochum)

A (slightly less) brief look into the restricted 3-body problem - Agustin Moreno
Members’ Colloquium Topic: A (slightly less) brief look into the restricted 3-body problem Speaker: Agustin Moreno Affiliation: Member, School of Mathematics Date: October 25, 2021 Despite the fact that the 3-body problem is an ancient conundrum that goes back to Newton, it is remarkabl
From playlist Members’ Colloquium

Joel Kamnitzer - Symplectic Resolutions, Coulomb Branches, and 3d Mirror Symmetry 1/5
In the 21st century, there has been a great interest in the study of symplectic resolutions, such as cotangent bundles of flag varieties, hypertoric varieties, quiver varieties, and affine Grassmannian slices. Mathematicians, especially Braden-Licata-Proudfoot-Webster, and physicists obser
From playlist 2021 IHES Summer School - Enumerative Geometry, Physics and Representation Theory

Higgs–Coulomb Correspondence and Wall-Crossing in Abelian GLSMs by Chiu-Chu Melissa Liu
PROGRAM: VORTEX MODULI ORGANIZERS: Nuno Romão (University of Augsburg, Germany) and Sushmita Venugopalan (IMSc, India) DATE & TIME: 06 February 2023 to 17 February 2023 VENUE: Ramanujan Lecture Hall, ICTS Bengaluru For a long time, the vortex equations and their associated self-dual fie
From playlist Vortex Moduli - 2023

Ex 2: The Difference Quotient (Quadratic Function)
This video provides an example of how to find the difference quotient for a quadratic function. Site: http://mathispower4u.com
From playlist Determining Function Values

Joel Kamnitzer - Symplectic Resolutions, Coulomb Branches, and 3d Mirror Symmetry 3/5
In the 21st century, there has been a great interest in the study of symplectic resolutions, such as cotangent bundles of flag varieties, hypertoric varieties, quiver varieties, and affine Grassmannian slices. Mathematicians, especially Braden-Licata-Proudfoot-Webster, and physicists obser
From playlist 2021 IHES Summer School - Enumerative Geometry, Physics and Representation Theory