
The Campbell-Baker-Hausdorff and Dynkin formula and its finite nature
In this video explain, implement and numerically validate all the nice formulas popping up from math behind the theorem of Campbell, Baker, Hausdorff and Dynkin, usually a.k.a. Baker-Campbell-Hausdorff formula. Here's the TeX and python code: https://gist.github.com/Nikolaj-K/8e9a345e4c932
From playlist Algebra

Probability - Quantum and Classical
The Law of Large Numbers and the Central Limit Theorem. Probability explained with easy to understand 3D animations. Correction: Statement at 13:00 should say "very close" to 50%.
From playlist Physics

Calculus - The Fundamental Theorem, Part 1
The Fundamental Theorem of Calculus. First video in a short series on the topic. The theorem is stated and two simple examples are worked.
From playlist Calculus - The Fundamental Theorem of Calculus

Intro to Bayes’s Theorem | Probability Theory
What is Bayes’s theorem for conditional probability? We'll be proving it briefly in today's lesson, as it is a direct result of the definition of conditional probabilities. We'll also see how Baye's theorem works with a sample space partitioned into separate events, and an example of apply
From playlist Probability Theory

Deriving Baye's Theorem | (Two) Minute Math with M³
Just a brief derivation of Baye's Theorem. A great probability theorem that needs some love! (Baye's Theorem = BAE)
From playlist Probability and Statistics

Probability: "At Least" Probabilities
This is the fourth video of a series from the Worldwide Center of Mathematics explaining the basics of probability. This video deals with calculating probabilities of "at least 1" or other "at least" probability calculations. For more math videos, visit our channel or go to www.centerofmat
From playlist Basics: Probability and Statistics

Guido Montúfar : Fisher information metric of the conditional probability politopes
Recording during the thematic meeting : "Geometrical and Topological Structures of Information" the September 01, 2017 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent
From playlist Geometry

Probability DISTRIBUTIONS for Discrete Random Variables (9-3)
A Probability Distribution: a mathematical description of (a) all possible outcomes for a random variable, and (b) the probabilities of each outcome occurring. Can be tabular (i.e., frequency table) or graphical (i.e., bar chart or histogram). For a discrete random variable, the underlying
From playlist Discrete Probability Distributions in Statistics (WK 9 - QBA 237)

(PP 6.1) Multivariate Gaussian - definition
Introduction to the multivariate Gaussian (or multivariate Normal) distribution.
From playlist Probability Theory

Anton Alekseev - The Kashiwara-Vergne theory and 2-dimensional topology
Abstract: The Kashiwara-Vergne problem is a property of the Baker-Campbell-Hausdorff series which was designed to study the Duflo Theorem in Lie theory. Surprisingly, it is related to many other fields of Mathematics including the Drinfled’s theory of associators and the theory of multipl
From playlist Algebraic Analysis in honor of Masaki Kashiwara's 70th birthday

The orbit method for (certain) pro-p groups (Lecture - 03) by Uri Onn
PROGRAM GROUP ALGEBRAS, REPRESENTATIONS AND COMPUTATION ORGANIZERS: Gurmeet Kaur Bakshi, Manoj Kumar and Pooja Singla DATE: 14 October 2019 to 23 October 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Determining explicit algebraic structures of semisimple group algebras is a fund
From playlist Group Algebras, Representations And Computation

Lie groups: Baker Campbell Hausdorff formula
This lecture is part of an online graduate course on Lie groups. We state the Baker Campbell Hausdorff formula for exp(A)exp(B). As applications we show that a Lie group is determined up to local isomorphism by its Lie algebra, and homomorphisms from a simply connected Lie group are deter
From playlist Lie groups
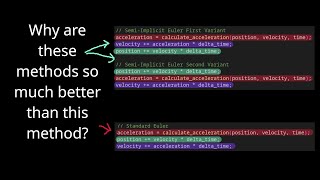
How to Come Up with the Semi-Implicit Euler Method Using Hamiltonian Mechanics #some2 #PaCE1
Notes for this video: https://josephmellor.xyz/downloads/symplectic-integrator-work.pdf When you first learn about Hamiltonian Mechanics, it seems like Lagrangian Mechanics with more work for less gain. The only reason we even learn Hamiltonian Mechanics in undergrad is that the Hamiltoni
From playlist Summer of Math Exposition 2 videos

The orbit method for (certain) pro-p groups (Lecture 2) by Uri Onn
PROGRAM GROUP ALGEBRAS, REPRESENTATIONS AND COMPUTATION ORGANIZERS: Gurmeet Kaur Bakshi, Manoj Kumar and Pooja Singla DATE: 14 October 2019 to 23 October 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Determining explicit algebraic structures of semisimple group algebras is a fund
From playlist Group Algebras, Representations And Computation

Prob & Stats - Bayes Theorem (1 of 24) What is Bayes Theorem?
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain what is and define the symbols of Bayes Theorem. Bayes Theorem calculates the probability of an event or the predictive value of an outcome of a test based on prior knowledge of condition rela
From playlist PROB & STATS 4 BAYES THEOREM

AKPotW: A Countable Set [Set Theory]
If this video is confusing, be sure to check out our blog for the full solution transcript! https://centerofmathematics.blogspot.com/2019/03/advanced-knowledge-problem-of-week-3-19.html
From playlist Center of Math: Problems of the Week

(PP 6.2) Multivariate Gaussian - examples and independence
Degenerate multivariate Gaussians. Some sketches of examples and non-examples of Gaussians. The components of a Gaussian are independent if and only if they are uncorrelated.
From playlist Probability Theory

Limit Theorems for Spatial Interacting Models by Yogeshwaran D
PROGRAM: TOPICS IN HIGH DIMENSIONAL PROBABILITY ORGANIZERS: Anirban Basak (ICTS-TIFR, India) and Riddhipratim Basu (ICTS-TIFR, India) DATE & TIME: 02 January 2023 to 13 January 2023 VENUE: Ramanujan Lecture Hall This program will focus on several interconnected themes in modern probab
From playlist TOPICS IN HIGH DIMENSIONAL PROBABILITY
