Spatial processes | Poisson point processes | Point processes | Lévy processes | Markov processes
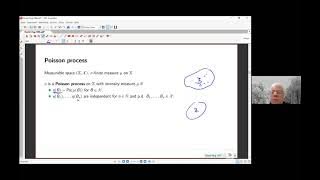
Poisson point process
In probability, statistics and related fields, a Poisson point process is a type of random mathematical object that consists of points randomly located on a mathematical space. The Poisson point process is often called simply the Poisson process, but it is also called a Poisson random measure, Poisson random point field or Poisson point field. This point process has convenient mathematical properties, which has led to its being frequently defined in Euclidean space and used as a mathematical model for seemingly random processes in numerous disciplines such as astronomy, biology, ecology, geology, seismology, physics, economics, image processing, and telecommunications. The process is named after French mathematician Siméon Denis Poisson despite Poisson's never having studied the process. Its name derives from the fact that if a collection of random points in some space forms a Poisson process, then the number of points in a region of finite size is a random variable with a Poisson distribution. The process was discovered independently and repeatedly in several settings, including experiments on radioactive decay, telephone call arrivals and insurance mathematics. The Poisson point process is often defined on the real line, where it can be considered as a stochastic process. In this setting, it is used, for example, in queueing theory to model random events, such as the arrival of customers at a store, phone calls at an exchange or occurrence of earthquakes, distributed in time. In the plane, the point process, also known as a spatial Poisson process, can represent the locations of scattered objects such as transmitters in a wireless network, particles colliding into a detector, or trees in a forest. In this setting, the process is often used in mathematical models and in the related fields of spatial point processes, stochastic geometry, spatial statistics and continuum percolation theory. The Poisson point process can be defined on more abstract spaces. Beyond applications, the Poisson point process is an object of mathematical study in its own right. In all settings, the Poisson point process has the property that each point is stochastically independent to all the other points in the process, which is why it is sometimes called a purely or completely random process. Despite its wide use as a stochastic model of phenomena representable as points, the inherent nature of the process implies that it does not adequately describe phenomena where there is sufficiently strong interaction between the points. This has inspired the proposal of other point processes, some of which are constructed with the Poisson point process, that seek to capture such interaction. The point process depends on a single mathematical object, which, depending on the context, may be a constant, a locally integrable function or, in more general settings, a Radon measure. In the first case, the constant, known as the rate or intensity, is the average density of the points in the Poisson process located in some region of space. The resulting point process is called a homogeneous or stationary Poisson point process. In the second case, the point process is called an inhomogeneous or nonhomogeneous Poisson point process, and the average density of points depend on the location of the underlying space of the Poisson point process. The word point is often omitted, but there are other Poisson processes of objects, which, instead of points, consist of more complicated mathematical objects such as lines and polygons, and such processes can be based on the Poisson point process. Both the homogeneous and nonhomogeneous Poisson point processes are particular cases of the generalized renewal process. (Wikipedia).