
👉Learn the basics of factoring quadratics by using different techniques. Some of the techniques used in factoring quadratics include: when the coefficient of the squared term is not 1. In that case, we first write the quadratic in standard form, next we multiply the coefficient of the squa
From playlist Factor Quadratic Expressions

Zero Factorial: Why is 0! = 1?
This video provides justification as to why 0!=1 using patterns and the meaning of a permutation. http://mathispower4u.com
From playlist Using the Binomial Theorem / Combinations

Factoring using difference of two squares, x^2 - 9, 16x^4 - 100y^2, 4(4x^4 - 25y^2)
👉Learn how to factor quadratics using the difference of two squares method. When a quadratic contains two terms where each of the terms can be expressed as the square of a number and the sign between the two terms is the minus sign, then the quadratic can be factored easily using the diffe
From playlist Factor Quadratic Expressions | Difference of Two Squares

From playlist Contributed talks One World Symposium 2020

Learn how to visualize factoring
👉Learn the basics of factoring quadratics by using different techniques. Some of the techniques used in factoring quadratics include: when the coefficient of the squared term is not 1. In that case, we first write the quadratic in standard form, next we multiply the coefficient of the squa
From playlist Factor Quadratic Expressions

Learning how to factor a binomial using the difference of two squares
👉Learn how to factor quadratics using the difference of two squares method. When a quadratic contains two terms where each of the terms can be expressed as the square of a number and the sign between the two terms is the minus sign, then the quadratic can be factored easily using the diffe
From playlist Factor Quadratic Expressions | Difference of Two Squares

Factoring a binomial using distributive property
👉Learn how to factor quadratics using the difference of two squares method. When a quadratic contains two terms where each of the terms can be expressed as the square of a number and the sign between the two terms is the minus sign, then the quadratic can be factored easily using the diffe
From playlist Factor Quadratic Expressions | Difference of Two Squares

But Why Does 0 Factorial Equal 1
Start your free 7 day trial with Blinkist and get 25% off of Premium membership: https://www.blinkist.com/bri Why does 0 factorial = 1 ? Let's answer this question! ►BECOME A CHANNEL MEMBER https://www.youtube.com/channel/UChVUSXFzV8QCOKNWGfE56YQ/join ►WEBSITE https://www.brithemathgu
From playlist Fun and Amazing Math

How to factor a binomial by factoring out the GCF as well as by difference of two squares
👉Learn how to factor quadratics using the difference of two squares method. When a quadratic contains two terms where each of the terms can be expressed as the square of a number and the sign between the two terms is the minus sign, then the quadratic can be factored easily using the diffe
From playlist Factor Quadratic Expressions | Difference of Two Squares

Roland Bauerschmidt - The Renormalisation Group - a Mathematical Perspective (2/4)
In physics, the renormalisation group provides a powerful point of view to understand random systems with strong correlations. Despite advances in a number of particular problems, in general its mathematical justification remains a holy grail. I will give an introduction to the main concep
From playlist Roland Bauerschmidt - The Renormalisation Group - a Mathematical Perspective

Probability and Random variables by VijayKumar Krishnamurthy
Winter School on Quantitative Systems Biology DATE: 04 December 2017 to 22 December 2017 VENUE: Ramanujan Lecture Hall, ICTS, Bengaluru The International Centre for Theoretical Sciences (ICTS) and the Abdus Salam International Centre for Theoretical Physics (ICTP), are organizing a Wint
From playlist Winter School on Quantitative Systems Biology

A Rigorous Renormalization Group Study of a p-Adic Quantum Field Theory
Abdelmalek Abdesselam University of Virginia November 12, 2010 ANALYSIS/MATHEMATICAL PHYSICS SEMINAR This talk will be a progress report on an ongoing research project which is joint work with Ajay Chandra and Gianluca Guadagni and which concerns a p-adic analog of the Brydges-Mitter-Scop
From playlist Mathematics

Statistical Mechanics Lecture 4
(April 23, 2013) Leonard Susskind completes the derivation of the Boltzman distribution of states of a system. This distribution describes a system in equilibrium and with maximum entropy. Originally presented in the Stanford Continuing Studies Program. Stanford University: http://www.st
From playlist Course | Statistical Mechanics

How do you factor using the difference of two squares
👉Learn the basics of factoring quadratics by using different techniques. Some of the techniques used in factoring quadratics include: when the coefficient of the squared term is not 1. In that case, we first write the quadratic in standard form, next we multiply the coefficient of the squa
From playlist Factor Quadratic Expressions

Perturbative QCD for colliders (pQCD - Lecture 4) by Michael Spira
PROGRAM THE MYRIAD COLORFUL WAYS OF UNDERSTANDING EXTREME QCD MATTER ORGANIZERS: Ayan Mukhopadhyay, Sayantan Sharma and Ravindran V DATE: 01 April 2019 to 17 April 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Strongly interacting phases of QCD matter at extreme temperature and
From playlist The Myriad Colorful Ways of Understanding Extreme QCD Matter 2019

Tides in binary star systems (Lecture - 01) by Tanja Hinderer
Summer School on Gravitational-Wave Astronomy DATE: 17 July 2017 to 28 July 2017 VENUE: Madhava Lecture Hall, ICTS Bangalore This school is a part of the annual ICTS summer schools in gravitational wave astronomy. This year’s school will focus on the physics and astrophysics of compact
From playlist Summer School on Gravitational-Wave Astronomy - 2017

The Permanents of Gaussian Matrices - Scott Aaronson
The Permanents of Gaussian Matrices - Scott Aaronson Massachusetts Institute of Technology November 29, 2010 In recent joint work with Alex Arkhipov, we proposed a quantum optics experiment, which would sample from a probability distribution that we believe cannot be sampled (even approxi
From playlist Mathematics

First injection ever of a 2 GeV beam in the CERN's Proton synchrotron
Live from the CERN Control Centre
From playlist CERN - the Laboratory
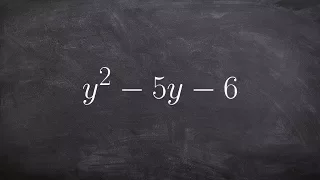
👉Learn how to factor quadratics. A quadratic is an algebraic expression having two as the highest power of its variable(s). To factor an algebraic expression means to break it up into expressions that can be multiplied together to get the original expression. To factor a quadratic with th
From playlist Factor Quadratic Expressions
Jon Keating: Random matrices, integrability, and number theory - Lecture 4
Abstract: I will give an overview of connections between Random Matrix Theory and Number Theory, in particular connections with the theory of the Riemann zeta-function and zeta functions defined in function fields. I will then discuss recent developments in which integrability plays an imp
From playlist Analysis and its Applications