
How to verify a trigonometric identity by factoring
👉 Learn how to verify Pythagoras trigonometric identities. A Pythagoras trigonometric identity is a trigonometric identity of the form sin^2 (x) + cos^2 (x) or any of its derivations. To verify trigonometric expression means to verify that the term(s) on the left-hand side of the equality
From playlist Verify Trigonometric Identities

Verifying Trigonometric Identities: The Fundamental Identities
Visit http://mathispower4u.wordpress.com/ for a categorized and searchable list of all videos.
From playlist Reciprocal, Quotient, Negative, and Pythagorean Trigonometric Identities
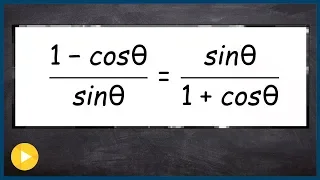
Verify an identity by multiplying by the conjugate
👉 Learn how to verify Pythagoras trigonometric identities. A Pythagoras trigonometric identity is a trigonometric identity of the form sin^2 (x) + cos^2 (x) or any of its derivations. To verify trigonometric expression means to verify that the term(s) on the left-hand side of the equality
From playlist Verify Trigonometric Identities

How to verify a trigonometric identity by using pythagorean identities
👉 Learn how to verify Pythagoras trigonometric identities. A Pythagoras trigonometric identity is a trigonometric identity of the form sin^2 (x) + cos^2 (x) or any of its derivations. To verify trigonometric expression means to verify that the term(s) on the left-hand side of the equality
From playlist Verify Trigonometric Identities

Trigonometry - Proving trig identities
Once you start getting a few more formulas and identities, you can use these to verify other identities. Watch this video for a few examples and some good tips when you have to verify a trigonometric identity. For more videos please visit http://www.mysecretmathtutor.com
From playlist Trigonometry

Verifying trigonometric identities by splitting up your fractions
👉 Learn how to verify Pythagoras trigonometric identities. A Pythagoras trigonometric identity is a trigonometric identity of the form sin^2 (x) + cos^2 (x) or any of its derivations. To verify trigonometric expression means to verify that the term(s) on the left-hand side of the equality
From playlist Verify Trigonometric Identities

Verifying an identity by multiplying
👉 Learn how to verify trigonometric identities by expanding the trigonometric expressions. When the given trigonometric expressions involve multiplications with more than one term in parenthesis, we start by expanding the expressions using the distributive property. After we have expande
From playlist Verify Trigonometric Identities

Verifying an identify by expanding an expression
👉 Learn how to verify trigonometric identities by expanding the trigonometric expressions. When the given trigonometric expressions involve multiplications with more than one term in parenthesis, we start by expanding the expressions using the distributive property. After we have expande
From playlist Verify Trigonometric Identities

How to verify a trigonometric identity
👉 Learn how to verify trigonometric identities by expanding the trigonometric expressions. When the given trigonometric expressions involve multiplications with more than one term in parenthesis, we start by expanding the expressions using the distributive property. After we have expande
From playlist Verify Trigonometric Identities

In this problem, I solve a neat matrix problem from a Romanian math competition, namely find all 2x2 matrices A such that A^3 - 3A^2 equals to the matrix whose entry is all -2. This is a beautiful application of linear algebra, more specifically traces and characteristic polynomials, enjoy
From playlist Linear Algebra

Linear Algebra 16L: Similarity Transformations Preserve the Trace and the Determinant
https://bit.ly/PavelPatreon https://lem.ma/LA - Linear Algebra on Lemma http://bit.ly/ITCYTNew - Dr. Grinfeld's Tensor Calculus textbook https://lem.ma/prep - Complete SAT Math Prep
From playlist Part 3 Linear Algebra: Linear Transformations
Linear Algebra II - Eigenvectors & eigenvalues: Oxford Maths 1st Year Student Lecture, James Maynard
In this lecture from James Maynard from his 1st Year Linear Algebra II course we introduce the idea of 'eigenvectors', which are vectors that are stretched by a linear transformation. Looking at eigenvectors gives a very useful perspective for understanding linear maps. You can access the
From playlist Oxford Mathematics 1st Year Student Lectures

The S3 character table - a (somewhat) new meaning | Diffusion Symmetry 2 | N J Wildberger
With diffusion symmetry, we explore mathematical objects or physical systems by spreading or diffusing from an initial point. The algebraic objects that result are hypergroups, or fusion algebra, or one of many similar and almost equivalent systems found in combinatorics, group theory, num
From playlist Diffusion Symmetry: A bridge between mathematics and physics

Spectral gap of random quantum channels - C. González-Guillén - Workshop 2 - CEB T3 2017
Carlos González-Guillén / 27.10.17 Spectral gap of random quantum channels We consider random quantum channels arising form uniform random isometries via the Stinespring representation. We will show that these channels are generically gapped, that is, there is a separation between the fi
From playlist 2017 - T3 - Analysis in Quantum Information Theory - CEB Trimester

Pre-recorded lecture 2: Nijenhuis torsion and its basic properties
MATRIX-SMRI Symposium: Nijenhuis Geometry and integrable systems Pre-recorded lecture: These lectures were recorded as part of a cooperation between the Chinese-Russian Mathematical Center (Beijing) and the Moscow Center of Fundamental and Applied Mathematics (Moscow). Nijenhuis Geomet
From playlist MATRIX-SMRI Symposium: Nijenhuis Geometry companion lectures (Sino-Russian Mathematical Centre)

Jesse Peterson: Von Neumann algebras and lattices in higher-rank groups, Lecture 1
Mini course of the conference YMC*A, August 2021, University of Münster. Lecture 1: Background on von Neumann algebras. Abstract: We’ll briskly review basic properties of semi-finite von Neumann algebras. The standard representation, completely positive maps, group von Neumann algebras, th
From playlist YMC*A 2021

An introduction to modified traces, Jonathan Kujawa, Lecture I
Lecture series on modified traces in algebra and topology The trace of a map and the dimension of a representation are fundamental invariants in representation theory. They are useful both for proving results in representation theory and for applications in other areas (e.g., low-dimensio
From playlist Lecture series on modified traces in algebra and topology

Peter Sarnak "Some analytic applications of the trace formula before and beyond endoscopy" [2012]
2012 FIELDS MEDAL SYMPOSIUM Date: October 17, 2012 11.00am-12.00pm We describe briefly some of the ways in which the trace formula has been used in a non comparative way. In particular we focus on families of automorphic L-functions symmetries associated with them which govern the distrib
From playlist Number Theory

How to verify a trig identity by factoring
👉 Learn how to verify Pythagoras trigonometric identities. A Pythagoras trigonometric identity is a trigonometric identity of the form sin^2 (x) + cos^2 (x) or any of its derivations. To verify trigonometric expression means to verify that the term(s) on the left-hand side of the equality
From playlist Verify Trigonometric Identities

Inna Zakharevich, Characteristic polynomials and traces
Global Noncommutative Geometry Seminar (Americas) on 10/22/21 https://globalncgseminar.org/talks/3584/
From playlist Global Noncommutative Geometry Seminar (Americas)