Tolerance interval

Statistical intervals | Statistical forecasting | Approximations

A tolerance interval is a statistical interval within which, with some confidence level, a specified proportion of a sampled population falls. "More specifically, a 100×p%/100×(1−α) tolerance interval provides limits within which at least a certain proportion (p) of the population falls with a given level of confidence (1−α)." "A (p, 1−α) tolerance interval (TI) based on a sample is constructed so that it would include at least a proportion p of the sampled population with confidence 1−α; such a TI is usually referred to as p-content − (1−α) coverage TI." "A (p, 1−α) upper tolerance limit (TL) is simply a 1−α upper confidence limit for the 100 p percentile of the population." A tolerance interval can be seen as a statistical version of a . "In the parameters-known case, a 95% tolerance interval and a 95% prediction interval are the same." If we knew a population's exact parameters, we would be able to compute a range within which a certain proportion of the population falls. For example, if we know a population is normally distributed with mean and standard deviation , then the interval includes 95% of the population (1.96 is the z-score for 95% coverage of a normally distributed population). However, if we have only a sample from the population, we know only the sample mean and sample standard deviation , which are only estimates of the true parameters. In that case, will not necessarily include 95% of the population, due to variance in these estimates. A tolerance interval bounds this variance by introducing a confidence level , which is the confidence with which this interval actually includes the specified proportion of the population. For a normally distributed population, a z-score can be transformed into a "k factor" or tolerance factor for a given via lookup tables or several approximation formulas. "As the degrees of freedom approach infinity, the prediction and tolerance intervals become equal." (Wikipedia).

Measuring Variation: Range and Standard Deviation

This lesson explains how to determine the range and standard deviation for a set of data. Site: http://mathispower4u.com

From playlist Statistics: Describing Data

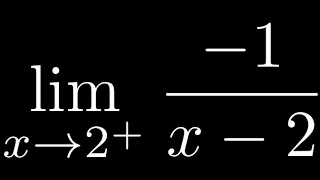
How to Compute a One Sided limit as x approaches from the right

In this video I will show you How to Compute a One Sided limit as x approaches from the right.

From playlist One-sided Limits

Limits and Continuity Practice Problems

From playlist Multivariable Calculus

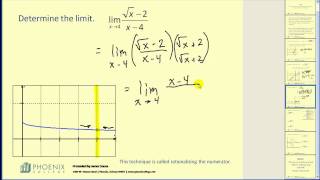
Part 1: Formal Definition of a Limit

This video states the formal definition of a limit and provide an epsilon delta proof that a limit exists. complete Video Library at http://www.mathispower4u.com

From playlist Limits

Maximum and Minimum Values (Closed interval method)

A review of techniques for finding local and absolute extremes, including an application of the closed interval method

From playlist 241Fall13Ex3

The Normal Distribution (1 of 3: Introductory definition)

More resources available at www.misterwootube.com

From playlist The Normal Distribution

The Range & Interquartile Range – Two Simple Measures of Variability (6-2)

We will begin with two simple measures of variability: the range and the interquartile range. Range is the variability between the two most extreme scores in the distribution. It is the difference between the largest and smallest scores. Outliers can affect the range, but not the interquar

From playlist WK6 Measures of Variability - Online Statistics for the Flipped Classroom

Computing Limits from a Graph with Infinities

In this video I do an example of computing limits from a graph with infinities.

From playlist Limits

Determining Limits

http://mathispower4u.wordpress.com/

From playlist Limits

CMPSC/Math 451: Feb. 23, 2015. Adaptive Simpson's Rule. Wen Shen

Wen Shen, Penn State University. Lectures are based on my book: "An Introduction to Numerical Computation", published by World Scientific, 2016. See promo video: https://youtu.be/MgS33HcgA_I

From playlist Numerical Computation spring 2015. Wen Shen. Penn State University.

Mathematica Tutorial 23 - The bisection method for solving an equation

In this Mathematica tutorial you will learn about the bisection method for solving an equation and how to use it. The bisection method is a slow but robust method for solving an equation numerically. *** SUBSCRIBE FOR MORE VIDEOS *** Never miss a daily video about Mathematics and Mathem

From playlist Mathematica Tutorials

ch4 A: Adaptive Simpson's Quadrature. Wen Shen

Wen Shen, Penn State University. Lectures are based on my book: "An Introduction to Numerical Computation", published by World Scientific, 2016. See promo video: https://youtu.be/MgS33HcgA_I

From playlist CMPSC/MATH 451 Videos. Wen Shen, Penn State University

Adaptive Quadrature | Lecture 41 | Vector Calculus for Engineers

What is adaptive quadrature? Join me on Coursera: https://www.coursera.org/learn/numerical-methods-engineers Lecture notes at http://www.math.ust.hk/~machas/numerical-methods-for-engineers.pdf Subscribe to my channel: http://www.youtube.com/user/jchasnov?sub_confirmation=1

From playlist Numerical Methods for Engineers

Live CEOing Ep 677: Language Design in Wolfram Language [Around, Min, & WFR Review]

In this episode of Live CEOing, Stephen Wolfram discusses upcoming improvements and features to the Wolfram Language. If you'd like to contribute to the discussion in future episodes, you can participate through this YouTube channel or through the official Twitch channel of Stephen Wolfram

From playlist Behind the Scenes in Real-Life Software Design

CMPSC/Math 451. Feb 27, 2015. Bisection method. Wen Shen

Wen Shen, Penn State University. Lectures are based on my book: "An Introduction to Numerical Computation", published by World Scientific, 2016. See promo video: https://youtu.be/MgS33HcgA_I

From playlist Numerical Computation spring 2015. Wen Shen. Penn State University.

Engineering CEE 20: Engineering Problem Solving. Lecture 8

UCI CIvil & Environmental Engineering 20 Engineering Problem Solving (Spring 2013) Lec 08. Engineering Problem Solving -- View the complete course: http://ocw.uci.edu/courses/cee_20_introduction_to_computational_engineering_problem_solving.html Instructor: Jasper Alexander Vrugt, Ph.D. L

From playlist Engineering CEE 20: Engineering Problem Solving

CMPSC/Math 451: March 2, 2015. Fixed point iterations. Wen Shen

Wen Shen, Penn State University. Lectures are based on my book: "An Introduction to Numerical Computation", published by World Scientific, 2016. See promo video: https://youtu.be/MgS33HcgA_I

From playlist Numerical Computation spring 2015. Wen Shen. Penn State University.

Adaptive Hierarchical Linear Spline Approximation

An introduction to adaptive hierarchical linear spline approximation using 1-dimensional examples. References: sparsegrids.org All animations were created using manim community version v0.9.0, a Python library for creating mathematical animations. See https://www.manim.community/ for mor

From playlist Summer of Math Exposition Youtube Videos

Engineering CEE 20: Engineering Problem Solving. Lecture 9

UCI CIvil & Environmental Engineering 20 Engineering Problem Solving (Spring 2013) Lec 09. Engineering Problem Solving -- View the complete course: http://ocw.uci.edu/courses/cee_20_introduction_to_computational_engineering_problem_solving.html Instructor: Jasper Alexander Vrugt, Ph.D.

From playlist Engineering CEE 20: Engineering Problem Solving

Closed Intervals, Open Intervals, Half Open, Half Closed

00:00 Intro to intervals 00:09 What is a closed interval? 02:03 What is an open interval? 02:49 Half closed / Half open interval 05:58 Writing in interval notation

From playlist Calculus

Tolerance interval

Related pages