
Introduction to Projective Geometry (Part 1)
The first video in a series on projective geometry. We discuss the motivation for studying projective planes, and list the axioms of affine planes.
From playlist Introduction to Projective Geometry
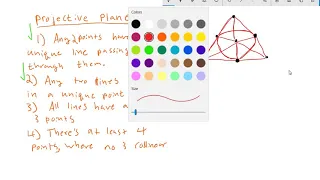
Introduction to Projective Geometry (Part 2)
The second video in a series about projective geometry. We list the axioms for projective planes, give an examle of a projective plane with finitely many points, and define the real projective plane.
From playlist Introduction to Projective Geometry

algebraic geometry 15 Projective space
This lecture is part of an online algebraic geometry course, based on chapter I of "Algebraic geometry" by Hartshorne. It introduces projective space and describes the synthetic and analytic approaches to projective geometry
From playlist Algebraic geometry I: Varieties
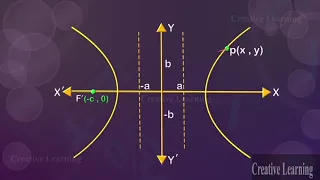
Hyperbola 3D Animation | Objective conic hyperbola | Digital Learning
Hyperbola 3D Animation In mathematics, a hyperbola is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, that are mirror images of each other an
From playlist Maths Topics

The circle and projective homogeneous coordinates (cont.) | Universal Hyperbolic Geometry 7b
Universal hyperbolic geometry is based on projective geometry. This video introduces this important subject, which these days is sadly absent from most undergrad/college curriculums. We adopt the 19th century view of a projective space as the space of one-dimensional subspaces of an affine
From playlist Universal Hyperbolic Geometry
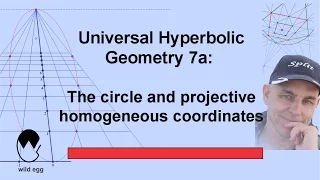
The circle and projective homogeneous coordinates | Universal Hyperbolic Geometry 7a | NJ Wildberger
Universal hyperbolic geometry is based on projective geometry. This video introduces this important subject, which these days is sadly absent from most undergrad/college curriculums. We adopt the 19th century view of a projective space as the space of one-dimensional subspaces of an affine
From playlist Universal Hyperbolic Geometry

Projective view of conics and quadrics | Differential Geometry 9 | NJ Wildberger
In this video we introduce projective geometry into the study of conics and quadrics. Our point of view follows Mobius and Plucker: the projective plane is considered as the space of one-dimensional subspaces of a three dimensional vector space, or in other words lines through the origin.
From playlist Differential Geometry

MATH331: Riemann Surfaces - part 1
We define what a Riemann Surface is. We show that PP^1 is a Riemann surface an then interpret our crazy looking conditions from a previous video about "holomorphicity at infinity" as coming from the definition of a Riemann Surface.
From playlist The Riemann Sphere
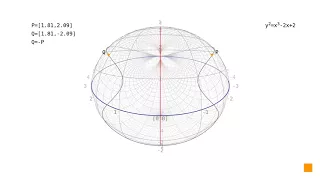
Elliptic curves: point at infinity in the projective plane
This video depicts point addition and doubling on elliptic curve in simple Weierstrass form in the projective plane depicted using stereographic projection where the point at infinity can actually be seen. Explanation is in the accompanying article https://trustica.cz/2018/04/05/elliptic-
From playlist Elliptic Curves - Number Theory and Applications

Fake projective planes by JongHae Keum
PROGRAM ZARISKI-DENSE SUBGROUPS AND NUMBER-THEORETIC TECHNIQUES IN LIE GROUPS AND GEOMETRY (ONLINE) ORGANIZERS: Gopal Prasad, Andrei Rapinchuk, B. Sury and Aleksy Tralle DATE: 30 July 2020 VENUE: Online Unfortunately, the program was cancelled due to the COVID-19 situation but it will
From playlist Zariski-dense Subgroups and Number-theoretic Techniques in Lie Groups and Geometry (Online)

Rigidity and Flexibility of Schubert classes - Colleen Robles
Colleen Robles Texas A & M University; Member, School of Mathematics January 27, 2014 Consider a rational homogeneous variety X. The Schubert classes of X form a free additive basis of the integral homology of X. Given a Schubert class S in X, Borel and Haefliger asked: aside from the Schu
From playlist Mathematics

Elisa Lorenzo Garcia : On smooth plane models for modular curves of Shimura type
CONFERENCE Recording during the thematic meeting : "COUNT, COmputations and their Uses in Number Theory" the February 27, 2023 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Jean Petit Find this video and other talks given by worldwide mathematici
From playlist Algebraic and Complex Geometry

Unexpected fillings, singularities, and plane curve arrangements - Laura Starkston
Joint IAS/Princeton/Montreal/Paris/Tel-Aviv Symplectic Geometry Topic: Unexpected fillings, singularities, and plane curve arrangements Speaker: Laura Starkston Affiliation: University of California, Davis Date: May 07, 2021 For more video please visit http://video.ias.edu
From playlist Mathematics

Tropical Geometry - Lecture 2 - Curve Counting | Bernd Sturmfels
Twelve lectures on Tropical Geometry by Bernd Sturmfels (Max Planck Institute for Mathematics in the Sciences | Leipzig, Germany) We recommend supplementing these lectures by reading the book "Introduction to Tropical Geometry" (Maclagan, Sturmfels - 2015 - American Mathematical Society)
From playlist Twelve Lectures on Tropical Geometry by Bernd Sturmfels

Christian Lehn: Symplectic varieties from cubic fourfolds
I will explain a construction of a family of 8-dimensional projective complex symplectic manifolds starting from the moduli space of twisted cubics on a general cubic fourfold. The relation to \mathrm{Hilb}^4 of a K3-surface is still open. This is a joint work with Manfred Lehn, Christoph
From playlist HIM Lectures: Junior Trimester Program "Algebraic Geometry"

Q-Homology Projective Planes by Jong-Hae Keum
Algebraic Surfaces and Related Topics PROGRAM URL : http://www.icts.res.in/program/AS2015 DESCRIPTION : This is a joint program of ICTS with TIFR, Mumbai and KIAS, Seoul. The theory of surfaces has been the cradle to many powerful ideas in Algebraic Geometry. The problems in this area
From playlist Algebraic Surfaces and Related Topics

Pierre Bieliavsky: Universal deformation twists from evolution equations
A universal twist (or "Drinfel'd Twist") based on a bi-algebra B consists in an element F of the second tensorial power of B that satisfies a certain cocycle condition. I will present a geometrical method to explicitly obtain such twists for a quite large class of examples where B underlie
From playlist HIM Lectures: Trimester Program "Non-commutative Geometry and its Applications"

Moduli Space of Curves by Chitrabhanu Chaudhuri
J-Holomorphic Curves and Gromov-Witten Invariants DATE:25 December 2017 to 04 January 2018 VENUE:Madhava Lecture Hall, ICTS, Bangalore Holomorphic curves are a central object of study in complex algebraic geometry. Such curves are meaningful even when the target has an almost complex stru
From playlist J-Holomorphic Curves and Gromov-Witten Invariants

The flexibility of caustics and its applications - Daniel Alvarez-Gavela
Workshop on the h-principle and beyond Topic: The flexibility of caustics and its applications Speaker: Daniel Alvarez-Gavela Affiliation: Massachusetts Institute of Technology Date: November 03, 2021 Alvarez-Gavela-2021-11-03 Singularities of smooth maps are flexible: there holds an h
From playlist Mathematics

Arithmetic Fake Compact Hermitian Symmetric Spaces - Gopal Prasad
Gopal Prasad University of Michigan February 16, 2012 A fake projective plane is a smooth complex projective algebraic surface whose Betti numbers are same as those of the complex projective plane but which is not the complex projective plane. The first fake projective plane was constructe
From playlist Mathematics