Ricci curvature

Curvature (mathematics) | Differential geometry | Riemannian manifolds | Tensors in general relativity | Riemannian geometry

In differential geometry, the Ricci curvature tensor, named after Gregorio Ricci-Curbastro, is a geometric object which is determined by a choice of Riemannian or pseudo-Riemannian metric on a manifold. It can be considered, broadly, as a measure of the degree to which the geometry of a given metric tensor differs locally from that of ordinary Euclidean space or pseudo-Euclidean space. The Ricci tensor can be characterized by measurement of how a shape is deformed as one moves along geodesics in the space. In general relativity, which involves the pseudo-Riemannian setting, this is reflected by the presence of the Ricci tensor in the Raychaudhuri equation. Partly for this reason, the Einstein field equations propose that spacetime can be described by a pseudo-Riemannian metric, with a strikingly simple relationship between the Ricci tensor and the matter content of the universe. Like the metric tensor, the Ricci tensor assigns to each tangent space of the manifold a symmetric bilinear form . Broadly, one could analogize the role of the Ricci curvature in Riemannian geometry to that of the Laplacian in the analysis of functions; in this analogy, the Riemann curvature tensor, of which the Ricci curvature is a natural by-product, would correspond to the full matrix of second derivatives of a function. However, there are other ways to draw the same analogy. In three-dimensional topology, the Ricci tensor contains all of the information which in higher dimensions is encoded by the more complicated Riemann curvature tensor. In part, this simplicity allows for the application of many geometric and analytic tools, which led to the solution of the Poincaré conjecture through the work of Richard S. Hamilton and Grigory Perelman. In differential geometry, lower bounds on the Ricci tensor on a Riemannian manifold allow one to extract global geometric and topological information by comparison (cf. comparison theorem) with the geometry of a constant curvature space form. This is since lower bounds on the Ricci tensor can be successfully used in studying the length functional in Riemannian geometry, as first shown in 1941 via Myers's theorem. One common source of the Ricci tensor is that it arises whenever one commutes the covariant derivative with the tensor Laplacian. This, for instance, explains its presence in the Bochner formula, which is used ubiquitously in Riemannian geometry. For example, this formula explains why the gradient estimates due to Shing-Tung Yau (and their developments such as the Cheng-Yau and Li-Yau inequalities) nearly always depend on a lower bound for the Ricci curvature. In 2007, John Lott, Karl-Theodor Sturm, and Cedric Villani demonstrated decisively that lower bounds on Ricci curvature can be understood entirely in terms of the metric space structure of a Riemannian manifold, together with its volume form. This established a deep link between Ricci curvature and Wasserstein geometry and optimal transport, which is presently the subject of much research. (Wikipedia).

Comparison geometry for Ricci curvature I, Guofang Wei [2016]

Slides for this talk: https://drive.google.com/open?id=1d3IhMz2enIsBOuKRPA6JF80FPqbHSR9v Ricci curvature occurs in the Einstein equation, Ricci flow, optimal transport, and is important both in mathematics and physics. Comparison method is one of the key tools in studying the Ricci curvat

From playlist Mathematics

Areejit Samal (7/25/22): Forman-Ricci curvature: A geometry-inspired measure with wide applications

Abstract: In the last few years, we have been active in the development of geometry-inspired measures for the edge-based characterization of real-world complex networks. In particular, we were first to introduce a discretization of the classical Ricci curvature proposed by R. Forman to the

From playlist Applied Geometry for Data Sciences 2022

Comparison geometry for Ricci curvature II, Guofang Wei [2016]

Slides for this talk: https://drive.google.com/open?id=1HN8y4H6IxwxEfiVyQNg1r9024Uwg4auO Ricci curvature occurs in the Einstein equation, Ricci flow, optimal transport, and is important both in mathematics and physics. Comparison method is one of the key tools in studying the Ricci curvat

From playlist Mathematics

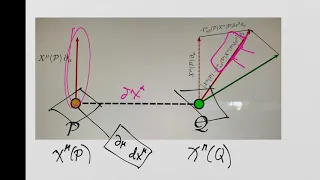
What is General Relativity? Lesson 51: The Ricci tensor examined

What is General Relativity? Lesson 51: The Ricci Tensor examined We study a calculation which demonstrates the significance of the Ricci tensor. The Ricci tensor provides a way to understand how fast an infinitesimal volume grows subject to free-fall motion in a curved spacetime. We we as

From playlist What is General Relativity?

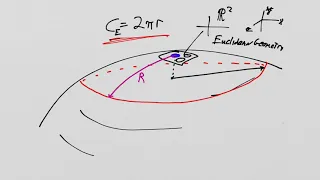
What is General Relativity? Lesson 59: Scalar Curvature Part 8: Interpretation of Scalar Curvature.

What is General Relativity? Lesson 59: Scalar Curvature Part 8: Interpretation of Scalar Curvature (note: this is a re-post of a video that was posted at 2x playback speed. Sorry!) We begin our examination of Section 4.4.6 of "A Simple Introduction to Particle Physics Part II - Geometric

From playlist What is General Relativity?

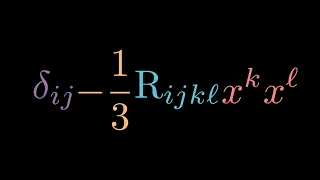
Curvature of a Riemannian Manifold | Riemannian Geometry

In this lecture, we define the exponential mapping, the Riemannian curvature tensor, Ricci curvature tensor, and scalar curvature. The focus is on an intuitive explanation of the curvature tensors. The curvature tensor of a Riemannian metric is a very large stumbling block for many student

From playlist All Videos

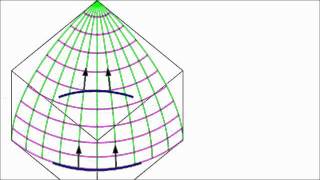
Relativity 7b4 - Riemann and Ricci tensors

The Riemann curvature tensor tells you everything there is to know about the curvature of spacetime. The Ricci tensor is derived from the Riemann tensor and describes changes in volume. It is the key object in Einstein's "field equations of general relativity."

From playlist Relativity - appendix videos

Ricci Curvature, Convexity and Applications - Aaron Naber [2011]

Name: Aaron Naber Event: Workshop on Extremal Kahler Metrics Event URL: view webpage Title: Ricci Curvature, Convexity and Applications Date: 2011-03-23 @9:30 AM Location: 102 http://scgp.stonybrook.edu/video_portal/video.php?id=611

From playlist Mathematics

Nicol Gigli - 22 September 2016

Gigli, Nicola "Spaces with Ricci curvature bounded from below: state of the art and future challenges."

From playlist A Mathematical Tribute to Ennio De Giorgi

Bruce KLEINER - Ricci flow, diffeomorphism groups, and the Generalized Smale Conjecture

The Smale Conjecture (1961) may be stated in any of the following equivalent forms: • The space of embedded 2-spheres in R3 is contractible. • The inclusion of the orthogonal group O(4) into the group of diffeomorphisms of the 3-sphere is a homotopy equivalence. • The s

From playlist Riemannian Geometry Past, Present and Future: an homage to Marcel Berger

Richard Hamilton | The Poincare Conjecture | 2006

The Poincare Conjecture Richard Hamilton Columbia University, New York, USA https://www.mathunion.org/icm/icm-videos/icm-2006-videos-madrid-spain/icm-madrid-videos-22082006

From playlist Number Theory

The Work of Grigory Perelman - John Lott [ICM 2006]

slides for this talk: https://www.mathunion.org/fileadmin/IMU/Videos/ICM2006/tars/laudationes2006_perelman.pdf The Work of Grigory Perelman John Lott University of Maryland, USA https://www.mathunion.org/icm/icm-videos/icm-2006-videos-madrid-spain/icm-madrid-videos-22082006

From playlist Mathematics

GPDE Workshop - Synthetic formulations - Cedric Villani

Cedric Villani IAS/ENS-France February 23, 2009 For more videos, visit http://video.ias.edu

From playlist Mathematics

Mokshay Madiman : Minicourse on information-theoretic geometry of metric measure

Recording during the thematic meeting : "Geometrical and Topological Structures of Information" the August 28, 2017 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematician

From playlist Geometry

Ancient solutions to geometric flows IV - Panagiota Daskalopoulos

Women and Mathematics: Uhlenbeck Lecture Course Topic: Ancient solutions to geometric flows IV Panagiota Daskalopoulos Affiliation: Columbia University Date: May 24, 2019 For more video please visit http://video.ias.edu

From playlist Mathematics

Ricci Flow - Numberphile

More links & stuff in full description below ↓↓↓ Ricci Flow was used to finally crack the Poincaré Conjecture. It was devised by Richard Hamilton but famously employed by Grigori Perelman in his acclaimed proof. It is named after mathematician Gregorio Ricci-Curbastro. In this video it i

From playlist Numberphile Videos

Ricci flows with Rough Initial Data - Peter Topping

Workshop on Geometric Functionals: Analysis and Applications Topic: Ricci flows with Rough Initial Data Speaker: Peter Topping Affiliation: University of Warwick Date: March 8, 2019 For more video please visit http://video.ias.edu

From playlist Mathematics

16/11/2015 - Jean-Pierre Bourguignon - General Relativity and Geometry

https://philippelefloch.files.wordpress.com/2015/11/2015-ihp-jpbourguignon.pdf Abstract. Physics and Geometry have a long history in common, but the Theory of General Relativity, and theories it triggered, have been a great source of challenges and inspiration for geometers. It started eve

From playlist 2015-T3 - Mathematical general relativity - CEB Trimester

Davide Barilari - Distorsion géodésique du volume et courbure de Ricci

On généralise le développement classique du volume riemannien le long du flot géodésique en terme de la courbure de Ricci au cas sous-riemannien (et plus généralement le long d'une classe de flots Hamiltoniens quadratiques). On introduit un nouvel invariant qui dénit l'interactio

From playlist Journée Sous-Riemannienne 2016

Ricci Curvature: Some Recent Progress and Open Questions - Jeff Cheeger [2016]

Slides for this talk: https://drive.google.com/open?id=1p9JK7EXKLyy_WxIfbrw02wjjoRm5E1je Name: Jeff Cheeger Event: Simons Collaboration on Special Holonomy Workshop Event URL: view webpage Title: Ricci Curvature: Some Recent Progress and Open Questions Date: 2016-09-09 @1:15 PM Location:

From playlist Mathematics

Ricci curvature

Related pages