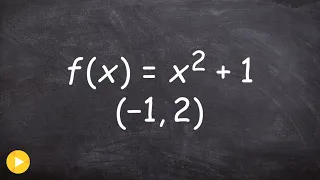
How to determine the absolute max min of a function on an open interval
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions
Calculus 1 Lecture 3.1 Part 6: Intervals of Increasing, Decreasing, and Concavity. How to Find Absolute Maximum and Absolute Minimum.
From playlist Calculus 1 Playlist 1
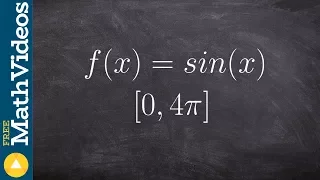
How to determine the max and min of a sine on a closed interval
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions
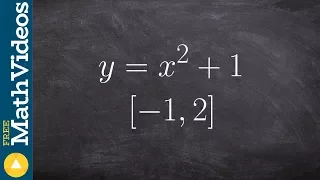
Find the max and min from a quadratic on a closed interval
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions
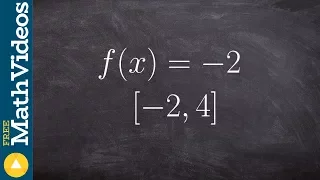
What is the max and min of a horizontal line on a closed interval
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions

http://mathispower4u.wordpress.com/
From playlist Differentiation Application - Absolute Extrema

Pre-Calculus - Identify the local maximum and minimum of a function
This video shows how to find the local maximum and minimum points when looking at the graph of a function. Remember that these are the maximum and minimum on some interval of the entire function. More specific techniques are covered for other functions like quadratics in later videos. F
From playlist Pre-Calculus
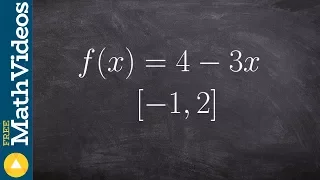
Find the max and min of a linear function on the closed interval
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions

Wen Shen, Penn State University. Lectures are based on my book: "An Introduction to Numerical Computation", published by World Scientific, 2016. See promo video: https://youtu.be/MgS33HcgA_I
From playlist CMPSC/MATH 451 Videos. Wen Shen, Penn State University

Lecture 16: The Min/Max Theorem and Bolzano's Intermediate Value Theorem
MIT 18.100A Real Analysis, Fall 2020 Instructor: Dr. Casey Rodriguez View the complete course: http://ocw.mit.edu/courses/18-100a-real-analysis-fall-2020/ YouTube Playlist: https://www.youtube.com/playlist?list=PLUl4u3cNGP61O7HkcF7UImpM0cR_L2gSw We prove some of the most useful tools of c
From playlist MIT 18.100A Real Analysis, Fall 2020

Liam Mazurowski - Recent developments in constant mean curvature hypersurfaces II
Continuing from the previous talk, we will first discuss two min-max theorems for constructing prescribed mean curvature hypersurfaces in non-compact spaces. The first concerns the existence of prescribed mean curvature hypersurfaces in Euclidean space, and the second concerns the existen
From playlist Not Only Scalar Curvature Seminar

Lecture 19: Differentiation Rules, Rolle's Theorem, and the Mean Value Theorem
MIT 18.100A Real Analysis, Fall 2020 Instructor: Dr. Casey Rodriguez View the complete course: http://ocw.mit.edu/courses/18-100a-real-analysis-fall-2020/ YouTube Playlist: https://www.youtube.com/playlist?list=PLUl4u3cNGP61O7HkcF7UImpM0cR_L2gSw We begin proving key properties of derivati
From playlist MIT 18.100A Real Analysis, Fall 2020

Calculus 1: Lecture 3.1 Extrema on an Interval
This is a real classroom Calculus 1 lecture. In this lecture I covered section 3.1 which is Extrema on an Interval. We talked about critical numbers, the extreme value theorem, and various other things. Lots of examples were done. I hope this helps someone.
From playlist Calculus 1 Full Lectures
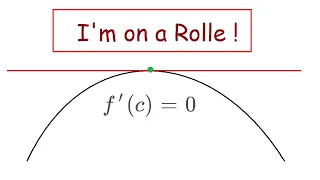
In this video, I prove Rolle’s theorem, which says that if f(a) = f(b), then there is a point c between a and b such that f’(c) = 0. This theorem is quintessential in proving the mean-value theorem in Calculus. Along the way I prove Fermat’s theorem, which says that if f has a maximum/mini
From playlist Real Analysis

Weyl Law for the phase transition spectrum and density of limit-interfaces - Marco Mendez Guaraco
Workshop on Mean Curvature and Regularity Topic: Weyl Law for the phase transition spectrum and density of limit-interfaces Speaker: Marco Mendez Guaraco Affiliation: Member, School of Mathematics Date: November 5, 2018 For more video please visit http://video.ias.edu
From playlist Workshop on Mean Curvature and Regularity

The Extreme Value Theorem and How to Use it in Calculus
The Extreme Value Theorem and How to Use it in Calculus The extreme value theorem is stated and then we do an example of finding the absolute extrema of a continuous function on a closed interval.
From playlist Calculus 1 Exam 2 Playlist

The min-max width of unit volume three-spheres - Lucas Ambrozio
Variational Methods in Geometry Seminar Topic: The min-max width of unit volume three-spheres Speaker: Lucas Ambrozio Affiliation: University of Warwick Affiliation: Member, School of Mathematics Date: November 20, 2018 For more video please visit http://video.ias.edu
From playlist Variational Methods in Geometry

How to determine the global max and min from a piecewise function
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions

Maria Esteban - Spectral results & open problems for Dirac-Coulomb operators w/ charge distributions
Recorded 12 April 2022. Maria J. Esteban of CNRS and Université Paris-Dauphine, Mathematics, presents "Spectral results and open problems for Dirac-Coulomb operators with general charge distributions" at IPAM's Model Reduction in Quantum Mechanics Workshop. Abstract: In this talk I will pr
From playlist 2022 Model Reduction in Quantum Mechanics Workshop
