Polynomials | Knot invariants | Knot theory
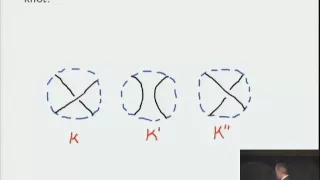
In the mathematical field of knot theory, the Jones polynomial is a knot polynomial discovered by Vaughan Jones in 1984. Specifically, it is an invariant of an oriented knot or link which assigns to each oriented knot or link a Laurent polynomial in the variable with integer coefficients. (Wikipedia).
Learn how to identify if a function is a polynomial and identify the degree and LC
👉 Learn how to determine whether a given equation is a polynomial or not. A polynomial function or equation is the sum of one or more terms where each term is either a number, or a number times the independent variable raised to a positive integer exponent. A polynomial equation of functio
From playlist Is it a polynomial or not?
Determining if a equation is a polynomial or not
👉 Learn how to determine whether a given equation is a polynomial or not. A polynomial function or equation is the sum of one or more terms where each term is either a number, or a number times the independent variable raised to a positive integer exponent. A polynomial equation of functio
From playlist Is it a polynomial or not?
Classify a polynomial then determining if it is a polynomial or not
👉 Learn how to determine whether a given equation is a polynomial or not. A polynomial function or equation is the sum of one or more terms where each term is either a number, or a number times the independent variable raised to a positive integer exponent. A polynomial equation of functio
From playlist Is it a polynomial or not?
Is it a polynomial with two variables
👉 Learn how to determine whether a given equation is a polynomial or not. A polynomial function or equation is the sum of one or more terms where each term is either a number, or a number times the independent variable raised to a positive integer exponent. A polynomial equation of functio
From playlist Is it a polynomial or not?
Determining if a function is a polynomial or not then determine degree and LC
👉 Learn how to determine whether a given equation is a polynomial or not. A polynomial function or equation is the sum of one or more terms where each term is either a number, or a number times the independent variable raised to a positive integer exponent. A polynomial equation of functio
From playlist Is it a polynomial or not?
How to Compute a Maclaurin Polynomial
Free ebook http://bookboon.com/en/learn-calculus-2-on-your-mobile-device-ebook What is a Maclaurin polynomial? In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point
From playlist A second course in university calculus.
Learn how to write a polynomial in standard form and classify
👉 Learn how to classify polynomials. A polynomial is an expression of the sums/differences of two or more terms having different integer exponents of the same variable. A polynomial can be classified in two ways: by the number of terms and by its degree. A monomial is an expression of 1
From playlist Classify Polynomials | Equations
Knots and Quantum Theory - Edward Witten
Edward Witten Institute for Advanced Study December 15, 2010 A knot is simply a tangled loop in ordinary three-dimensional space, such as often causes us frustration in everyday life. Knots are also the subject of a rather rich mathematical theory. In the last three decades, it has unexpec
From playlist Natural Sciences
Knots and Quantum Theory | Edward Witten, Charles Simonyi Professor
Edward Witten, Charles Simonyi Professor, School of Natural Sciences, Institute for Advanced Study http://www.ias.edu/people/faculty-and-emeriti/witten A knot is more or less what you think it is—a tangled mess of string in ordinary three-dimensional space. In the twentieth century, mathe
From playlist Natural Sciences
A refined upper bound for the volume...Jones polynomial - Anastasiia Tsvietkova
Anastasiia Tsvietkova, UC Davis October 8, 2015 http://www.math.ias.edu/wgso3m/agenda 2015-2016 Monday, October 5, 2015 - 08:00 to Friday, October 9, 2015 - 12:00 This workshop is part of the topical program "Geometric Structures on 3-Manifolds" which will take place during the 2015-2016
From playlist Workshop on Geometric Structures on 3-Manifolds
Knots, Virtual Knots and Virtual Knot Cobordism by Louis H. Kauffman
PROGRAM KNOTS THROUGH WEB (ONLINE) ORGANIZERS: Rama Mishra, Madeti Prabhakar, and Mahender Singh DATE & TIME: 24 August 2020 to 28 August 2020 VENUE: Online Due to the ongoing COVID-19 pandemic, the original program has been canceled. However, the meeting will be conducted through onl
From playlist Knots Through Web (Online)
Learn how to classify and identify the lc and degree of a polynomial
👉 Learn how to classify polynomials. A polynomial is an expression of the sums/differences of two or more terms having different interger exponents of the same variable. A polynomial can be classified in two ways: by the number of terms and by its degree. A monomial is an expression of 1
From playlist Classify Polynomials
How to reorder and classify a polynomial based on it's degree and number of terms
👉 Learn how to classify polynomials. A polynomial is an expression of the sums/differences of two or more terms having different integer exponents of the same variable. A polynomial can be classified in two ways: by the number of terms and by its degree. A monomial is an expression of 1
From playlist Classify Polynomials | Equations
Non-Orientable Knot Genus and the Jones Polynomial - Efstratia Kalfagianni
Efstratia Kalfagianni Michigan State University October 20, 2015 https://www.math.ias.edu/seminars/abstract?event=89714 The non-orientable genus (a.k.a crosscap number) of a knot is the smallest genus over all non-orientable surfaces spanned by the knot. In this talk, I’ll describe joint
From playlist Geometric Structures on 3-manifolds
Ed Witten -- From Gauge Theory to Khovanov Homology Via Floer Theory
Edward Witten lecture entitled "From Gauge Theory to Khovanov Homology Via Floer Theory" as part of the Banff International Research Station conference "Perspectives on Knot Homology". The Banff International Research Station will host the "Perspectives on Knot Homology" workshop in Banf
From playlist Research Lectures
Sir Michael Atiyah - The Mysteries of Space [1991]
The 64th annual Gibbs Lecture was given by Sir Michael Atiyah, Fellow of the Royal Society, of Trinity College, Cambridge, England. At a conference in San Francisco, California in January 1991, he delivered "Physics and the mysteries of space", which was filmed and made available on videot
From playlist Mathematics
Stavros Garoufalidis - Arithmetic Resurgence of Quantum Invariants
I will explain some conjectures concerning arithmetic resurgence of quantum knot and 3-manifold invariants formulated in an earlier work of mine in 2008, as well as numerical tests of those conjectures and their relations to quantum modular forms, state integrals and their q-series. Joint
From playlist Resurgence in Mathematics and Physics
Paul Turner: A hitchhiker's guide to Khovanov homology - Part I
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Geometry
Free ebook http://tinyurl.com/EngMathYT A lecture showing how to compute Taylor polynomials. Plenty of examples are discussed and solved. Such ideas are used in approximation of functions and are seen in university mathematics.
From playlist A second course in university calculus.