Manifolds | Links (knot theory)
Link (knot theory)
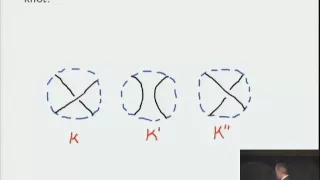
In mathematical knot theory, a link is a collection of knots which do not intersect, but which may be linked (or knotted) together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory. Implicit in this definition is that there is a trivial reference link, usually called the unlink, but the word is also sometimes used in context where there is no notion of a trivial link. For example, a co-dimension 2 link in 3-dimensional space is a subspace of 3-dimensional Euclidean space (or often the 3-sphere) whose connected components are homeomorphic to circles. The simplest nontrivial example of a link with more than one component is called the Hopf link, which consists of two circles (or unknots) linked together once. The circles inthe Borromean rings are collectively linked despite the fact that no two of them are directly linked. The Borromean rings thus form a Brunnian link and in fact constitute the simplest such link. (Wikipedia).