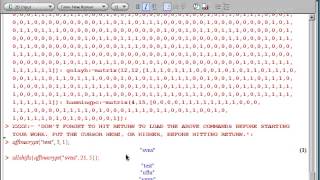
How to encrypt and decrypt the affine cipher using Maple software. Code from Into to Crypto and Coding Theory 2nd ed. by W. Trappe and LC Washington.
From playlist Cryptography and Coding Theory

Affine Cipher - Decryption (Known Plaintext Attack)
In this video I talk about ways to decrypt the Affine Cipher when the key is NOT known. Specifically, I go over an example of the known plaintext attack. 3^(-1) = 9 (mod 26) math worked out (Euclidean Algorithm): 1. Forwards: 26 = 3(8) + 2 3 = 2(1) + 1 2. Backwords: 1 = 3 -
From playlist Cryptography and Coding Theory

What are affine transformations?
Algorithm Archive: https://www.algorithm-archive.org/contents/affine_transformations/affine_transformations.html Github sponsors (Patreon for code): https://github.com/sponsors/leios Patreon: https://www.patreon.com/leiosos Twitch: https://www.twitch.tv/leioslabs Discord: https://discor
From playlist Algorithm Archive
Novel Algebraic Operations for Affine Geometry | Algebraic Calculus One | Wild Egg
We introduce some novel conventions to help us set up the foundations of affine geometry. We learn about differences of points, sums of points and vectors, affine combinations and vector proportions. And then use these to state a number of important results from affine geometry, including
From playlist Algebraic Calculus One from Wild Egg

Affine and mod-affine varieties in arithmetic geometry. - Charles - Workshop 2 - CEB T2 2019
François Charles (Université Paris-Sud) / 24.06.2019 Affine and mod-affine varieties in arithmetic geometry. We will explain how studying arithmetic versions of affine schemes and their bira- tional modifications leads to a generalization to arbitrary schemes of both Fekete’s theorem on
From playlist 2019 - T2 - Reinventing rational points
Combinatorial affine sieve - Alireza Salehi Golsefidy
Speaker: Alireza Salehi Golsefidy (UCSD) Title: Combinatorial affine sieve Abstract: In this talk the general setting of affine sieve will be presented. Next I will explain the Bourgain-Gamburd-Sarnak method on proving affine sieve in the presence of certain spectral gap. Finally I will sa
From playlist Mathematics

Affine Transformations — Topic 27 of Machine Learning Foundations
In this video we use hands-on code demos in NumPy to carry out affine transformations, a particular type of matrix transformation that may adjust angles or distances between vectors, but preserves parallelism. These operations can transform the target tensor in a variety of ways including
From playlist Linear Algebra for Machine Learning

algebraic geometry 5 Affine space and the Zariski topology
This lecture is part of an online algebraic geometry course, based on chapter I of "Algebraic geometry" by Hartshorne. It covers the definition of affine space and its Zariski topology.
From playlist Algebraic geometry I: Varieties

Cryptanalysis of Classical Ciphers
Cryptography and Network Security by Prof. D. Mukhopadhyay, Department of Computer Science and Engineering, IIT Kharagpur. For more details on NPTEL visit http://nptel.iitm.ac.in
From playlist Computer - Cryptography and Network Security

Cryptography and Network Security by Prof. D. Mukhopadhyay, Department of Computer Science and Engineering, IIT Kharagpur. For more details on NPTEL visit http://nptel.iitm.ac.in
From playlist Computer - Cryptography and Network Security
Calculus and affine geometry of the magical parabola | Algebraic Calc and dCB curves 3 | Wild Egg
Algebraic Calculus naturally lives in affine geometry, not Euclidean geometry. Affine geometry is the geometry of parallelism, or (almost the same thing) --- the geometry of pure linear algebra. The parabola is characterized projectively in this geometry as the unique conic which is tangen
From playlist Algebraic Calculus One Info

Math for Liberal Studies - Lecture 3.8.1 Affine and Multiplicative Ciphers
This is the first video lecture for Math for Liberal Studies, Section 3.8: More Modular Arithmetic and Public-Key Cryptography. In this lecture, I talk about how we can use multiplication in modular arithmetic to construct new ciphers. I also discuss the difficulty in finding the decryptio
From playlist Math for Liberal Studies Lectures

Cryptography I, Lecture 1: Classical ciphers
From playlist Crypto1

Cryptography Lecture 2, Substitution Ciphers
From playlist Calculus I

Group Theory for Cryptology by Carlo Scoppola
PROGRAM GROUP ALGEBRAS, REPRESENTATIONS AND COMPUTATION ORGANIZERS: Gurmeet Kaur Bakshi, Manoj Kumar and Pooja Singla DATE: 14 October 2019 to 23 October 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Determining explicit algebraic structures of semisimple group algebras is a fund
From playlist Group Algebras, Representations And Computation
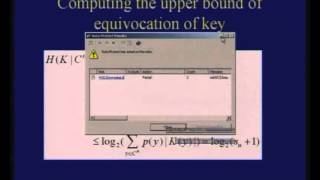
Cryptography and Network Security by Prof. D. Mukhopadhyay, Department of Computer Science and Engineering, IIT Kharagpur. For more details on NPTEL visit http://nptel.iitm.ac.in
From playlist Computer - Cryptography and Network Security

algebraic geometry 17 Affine and projective varieties
This lecture is part of an online algebraic geometry course, based on chapter I of "Algebraic geometry" by Hartshorne. It covers the relation between affine and projective varieties, with some examples such as a cubic curve and the twisted cubic.
From playlist Algebraic geometry I: Varieties
Cryptography and Network Security by Prof. D. Mukhopadhyay, Department of Computer Science and Engineering, IIT Kharagpur. For more details on NPTEL visit http://nptel.iitm.ac.in
From playlist Computer - Cryptography and Network Security