
Math 060 Fall 2017 111317C Orthonormal Bases
Motivation: how to obtain the coordinate vector with respect to a given basis? Definition: orthogonal set. Example. Orthogonal implies linearly independent. Orthonormal sets. Example of an orthonormal set. Definition: orthonormal basis. Properties of orthonormal bases. Example: Fou
From playlist Course 4: Linear Algebra (Fall 2017)

Dual basis definition and proof that it's a basis In this video, given a basis beta of a vector space V, I define the dual basis beta* of V*, and show that it's indeed a basis. We'll see many more applications of this concept later on, but this video already shows that it's straightforwar
From playlist Dual Spaces

Linear Algebra for Computer Scientists. 7. Linear Combinations of Vectors
This computer science video is one of a series on linear algebra for computer scientists. In this video you will learn about linear combinations of vectors, that is, you will learn how to create new vectors by scaling then adding other vectors together. You will also learn that some sets
From playlist Linear Algebra for Computer Scientists

Orthogonal bases are easy to work with!
Description: We can extend the idea of two orthogonal vectors to an orthogonal set of vectors. Then, if you have an orthogonal basis opposed to a normal basis, trying to expand a vector in the basis is a much easier task; each coefficient is determined by a couple dot products only. Lear
From playlist Linear Algebra (Full Course)

35 - Properties of bases (continued)
Algebra 1M - international Course no. 104016 Dr. Aviv Censor Technion - International school of engineering
From playlist Algebra 1M

Linear Algebra: Orthonormal Basis
Learn the basics of Linear Algebra with this series from the Worldwide Center of Mathematics. Find more math tutoring and lecture videos on our channel or at http://centerofmath.org/ More on unit vectors: https://www.youtube.com/watch?v=C6EYJVBYXIo
From playlist Basics: Linear Algebra

From playlist Linear Algebra Ch 8 (updated Jan2021)

Linear Algebra: Given an orthonormal basis of R^n, we present a quick method for finding coefficients of linear combination in terms of the basis. We also give an analogue of Parseval's Identity, which relates these coefficients to the squared length of the vector.
From playlist MathDoctorBob: Linear Algebra I: From Linear Equations to Eigenspaces | CosmoLearning.org Mathematics

General Vector Spaces and Tensors | Wrap it Up!
In this video, I will introduce general vectorspaces over fields, the dual vectorspace, the cobasis, and general tensors. Translate This Video : http://www.youtube.com/timedtext_video?ref=share&v=1ReUzrT8n_Q Notes : None yet Patreon : https://www.patreon.com/user?u=16481182 Teespring : ht
From playlist Wrap It Up!

[Lesson 1] QED Prerequisites Dirac Formalism Part I (redux)
(Editorial repair made in this version) This lecture is the first in a series of topics related to QED prerequisite material. I will be selecting some topics that students are often not clear about when arriving at QED. These topics cover a wide variety of material in elementary quantum m
From playlist QED- Prerequisite Topics

Vector Spaces andt Tensors | Wrap it Up!
In this video, I will summarize general vectorspaces on fields, bases, the dual vectorspace, and tensors/their components. This includes the dual basis definition. Translate This Video: Email : fematikaqna@gmail.com Discord: https://discord.gg/5z7pgj5 Subreddit : https://www.reddit.com/r/
From playlist Wrap It Up!

What is a Tensor? Lesson 26: P-vectors and P-forms Recap
What is a Tensor? Lesson 26: P-vectors and P-forms Recap I'm struggling with this complex topic. I don't like any of the other lessons on p-forms so I am going to keep trying till I get it right. This little "recap" re-does a few topics and introduces the idea of p-vectors.
From playlist What is a Tensor?
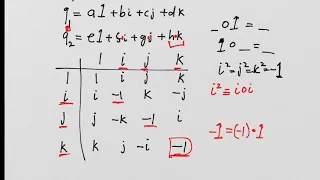
Lie Groups and Lie Algebras: Lesson 2 - Quaternions
This video is about Lie Groups and Lie Algebras: Lesson 2 - Quaternions We study the algebraic nature of quaternions and cover the ideas of an algebra and a field. Later we will discover how quaternions fit into the description of the classical Lie Groups. NOTE: An astute viewer noted th
From playlist Lie Groups and Lie Algebras

What is a Tensor Lesson #2: How to make a map.
This video is about What is a Tensor Lesson #2: How to make a map.
From playlist What is a Tensor?

Additive Number Theory: Extremal Problems and the Combinatorics....(Lecture 2) by M. Nathanson
Program Workshop on Additive Combinatorics ORGANIZERS: S. D. Adhikari and D. S. Ramana DATE: 24 February 2020 to 06 March 2020 VENUE: Madhava Lecture Hall, ICTS Bangalore Additive combinatorics is an active branch of mathematics that interfaces with combinatorics, number theory, ergod
From playlist Workshop on Additive Combinatorics 2020
Tensor Calculus 6b: The Covariant Derivative
This course will eventually continue on Patreon at http://bit.ly/PavelPatreon Textbook: http://bit.ly/ITCYTNew Errata: http://bit.ly/ITAErrata McConnell's classic: http://bit.ly/MCTensors Table of Contents of http://bit.ly/ITCYTNew Rules of the Game Coordinate Systems and the Role of Te
From playlist Introduction to Tensor Calculus

Additive Number Theory: Extremel Problems and the Combinatorics....(Lecture 3) by M. Nathanson
Program Workshop on Additive Combinatorics ORGANIZERS: S. D. Adhikari and D. S. Ramana DATE: 24 February 2020 to 06 March 2020 VENUE: Madhava Lecture Hall, ICTS Bangalore Additive combinatorics is an active branch of mathematics that interfaces with combinatorics, number theory, ergod
From playlist Workshop on Additive Combinatorics 2020
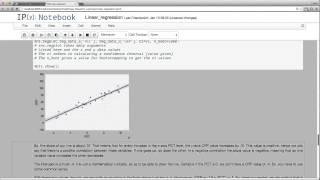
Linear regression is used to compare sets or pairs of numerical data points. We use it to find a correlation between variables.
From playlist Learning medical statistics with python and Jupyter notebooks

