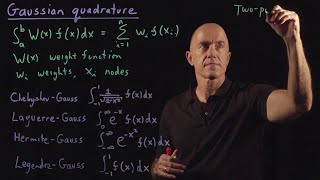Numerical integration (quadrature)
Adaptive quadrature is a numerical integration method in which the integral of a function is approximated using static quadrature rules on adaptively refined subintervals of the region of integration. Generally, adaptive algorithms are just as efficient and effective as traditional algorithms for "well behaved" integrands, but are also effective for "badly behaved" integrands for which traditional algorithms may fail. (Wikipedia).
Adaptive Quadrature | Lecture 41 | Vector Calculus for Engineers
What is adaptive quadrature? Join me on Coursera: https://www.coursera.org/learn/numerical-methods-engineers Lecture notes at http://www.math.ust.hk/~machas/numerical-methods-for-engineers.pdf Subscribe to my channel: http://www.youtube.com/user/jchasnov?sub_confirmation=1
From playlist Numerical Methods for Engineers
Gaussian Quadrature | Lecture 40 | Numerical Methods for Engineers
An explanation of Gaussian quadrature. An example of how to calculate the weights and nodes for two-point Legendre-Gauss quadrature. Join me on Coursera: https://www.coursera.org/learn/numerical-methods-engineers Lecture notes at http://www.math.ust.hk/~machas/numerical-methods-for-engi
From playlist Numerical Methods for Engineers
Adding Vectors Geometrically: Dynamic Illustration
Link: https://www.geogebra.org/m/tsBer5An
From playlist Trigonometry: Dynamic Interactives!
This video introduces the concept of phased arrays. An array refers to multiple sensors, arranged in some configuration, that act together to produce a desired sensor pattern. With a phased array, we can electronically steer that pattern without having to physically move the array simply b
From playlist Understanding Phased Array Systems and Beamforming
Computational Methods for Numerical Relativity, Part 3 Frans Pretorius
Computational Methods for Numerical Relativity, Part 3 Frans Pretorius Princeton University July 22, 2009
From playlist PiTP 2009
An introduction to Beamforming
This video talks about how we actually have more control over the shape of the beam than just adding additional elements or adjusting the position and orientation of the elements. We can also adjust the gain of the signal to each element and apply phase unevenly to each element, and that
From playlist Understanding Phased Array Systems and Beamforming
Ditch the Tricks: Estimating Trig Ratios: Conceptual Quiz Questions
Link: https://www.geogebra.org/m/F5a9GDd6
From playlist Trigonometry: Dynamic Interactives!
Engineering CEE 20: Engineering Problem Solving. Lecture 24
UCI CIvil & Environmental Engineering 20 Engineering Problem Solving (Spring 2013) Lec 24. Engineering Problem Solving View the complete course: http://ocw.uci.edu/courses/cee_20_introduction_to_computational_engineering_problem_solving.html Instructor: Jasper Alexander Vrugt, Ph.D. Licen
From playlist Engineering CEE 20: Engineering Problem Solving
DDPS | Towards reliable, efficient, and automated model reduction of parametrized nonlinear PDEs
Description: Many engineering tasks, such as parametric study and uncertainty quantification, require rapid and reliable solution of partial differential equations (PDEs) for many different configurations. In this talk, we consider goal-oriented model reduction of parametrized nonlinear PD
From playlist Data-driven Physical Simulations (DDPS) Seminar Series
Continuous multi-fidelity optimization
This video is #8 in the Adaptive Experimentation series presented at the 18th IEEE Conference on eScience in Salt Lake City, UT (October 10-14, 2022). In this video, Sterling Baird @sterling-baird presents on continuous multifidelity optimization. Continuous multi-fidelity optimization is
From playlist Optimization tutorial
Cyclic Quadrilateral: Proof Hint!
Link: https://www.geogebra.org/m/KYdypjws
From playlist Geometry: Dynamic Interactives!
Tzanio Kolev - Meso and Macroscale Modeling 1 - IPAM at UCLA
Recorded 15 March 2023. Tzanio Kolev of Lawrence Livermore National Laboratory presents "Meso and Macroscale Modeling 1" at IPAM's New Mathematics for the Exascale: Applications to Materials Science Tutorials. Learn more online at: http://www.ipam.ucla.edu/programs/workshops/new-mathematic
From playlist 2023 New Mathematics for the Exascale: Applications to Materials Science Tutorials
Lin Lin - Large scale hybrid DFT functionals: fast algorithms and finite-size effects - IPAM at UCLA
Recorded 02 May 2022. Lin Lin of the University of California, Berkeley, Mathematics, presents "Large scale hybrid DFT functionals: fast algorithms and finite-size effects" at IPAM's Large-Scale Certified Numerical Methods in Quantum Mechanics Workshop. Abstract: I will discuss recent prog
From playlist 2022 Large-Scale Certified Numerical Methods in Quantum Mechanics
CMPSC/Math 451: Feb. 23, 2015. Adaptive Simpson's Rule. Wen Shen
Wen Shen, Penn State University. Lectures are based on my book: "An Introduction to Numerical Computation", published by World Scientific, 2016. See promo video: https://youtu.be/MgS33HcgA_I
From playlist Numerical Computation spring 2015. Wen Shen. Penn State University.
Daniele Avitabile - Projection methods for neurobiological networks
---------------------------------- Institut Henri Poincaré, 11 rue Pierre et Marie Curie, 75005 PARIS http://www.ihp.fr/ Rejoingez les réseaux sociaux de l'IHP pour être au courant de nos actualités : - Facebook : https://www.facebook.com/InstitutHenriPoincare/ - Twitter : https://twitter
From playlist Workshop "Workshop on Mathematical Modeling and Statistical Analysis in Neuroscience" - January 31st - February 4th, 2022
FFT based spectral Ewald methods as an alternative to multipole methods – A.-K. Tornberg – ICM2018
Numerical Analysis and Scientific Computing Invited Lecture 15.5 FFT based spectral Ewald methods as an alternative to fast multipole methods Anna-Karin Tornberg Abstract: In this paper, we review a set of fast and spectrally accurate methods for rapid evaluation of three dimensional ele
From playlist Numerical Analysis and Scientific Computing
Scott Field - Gravitational Wave Parameter Estimation with Compressed Likelihood Evaluations
Recorded 17 November 2021. Scott Field of the University of Massachusetts Dartmouth presents "Gravitational Wave Parameter Estimation with Compressed Likelihood Evaluations" at IPAM's Workshop III: Source inference and parameter estimation in Gravitational Wave Astronomy. Abstract: One of
From playlist Workshop: Source inference and parameter estimation in Gravitational Wave Astronomy
Composite Quadrature Rules | Lecture 39 | Numerical Methods for Engineers
Composite quadrature rules (numerical integration) using the trapezoidal rule and Simpson's rule. Join me on Coursera: https://www.coursera.org/learn/numerical-methods-engineers Lecture notes at http://www.math.ust.hk/~machas/numerical-methods-for-engineers.pdf Subscribe to my channel:
From playlist Numerical Methods for Engineers
