
Algebraic Structures: Groups, Rings, and Fields
This video covers the definitions for some basic algebraic structures, including groups and rings. I give examples of each and discuss how to verify the properties for each type of structure.
From playlist Abstract Algebra

Data Structures: List as abstract data type
See complete series of videos in data structures here: http://www.youtube.com/playlist?list=PL2_aWCzGMAwI3W_JlcBbtYTwiQSsOTa6P&feature=view_all In this lesson, we will introduce a dynamic list structure as an abstract data type and then see one possible implementation of dynamic list using
From playlist Data structures

An Introduction to Abstract Data Types ADT Data Structures Source Code: https://github.com/williamfiset/algorithms My website: http://www.williamfiset.com =================================== Practicing for interviews? I have used, and recommend `Cracking the Coding Interview` which go
From playlist Data structures playlist

Now that we know what a quotient group is, let's take a look at an example to cement our understanding of the concepts involved.
From playlist Abstract algebra

Group Definition (expanded) - Abstract Algebra
The group is the most fundamental object you will study in abstract algebra. Groups generalize a wide variety of mathematical sets: the integers, symmetries of shapes, modular arithmetic, NxM matrices, and much more. After learning about groups in detail, you will then be ready to contin
From playlist Abstract Algebra

An introduction to abstract algebra | Abstract Algebra Math Foundations 213 | NJ Wildberger
How do we set up abstract algebra? In other words, how do we define basic algebraic objects such as groups, rings, fields, vector spaces, algebras, lattices, modules, Lie algebras, hypergroups etc etc?? This is a hugely important question, and not an easy one to answer. In this video we s
From playlist Math Foundations

What is a Group? | Abstract Algebra
Welcome to group theory! In today's lesson we'll be going over the definition of a group. We'll see the four group axioms in action with some examples, and some non-examples as well which violate the axioms and are thus not groups. In a fundamental way, groups are structures built from s
From playlist Abstract Algebra

What is Abstract Algebra? (Modern Algebra)
Abstract Algebra is very different than the algebra most people study in high school. This math subject focuses on abstract structures with names like groups, rings, fields and modules. These structures have applications in many areas of mathematics, and are being used more and more in t
From playlist Abstract Algebra

Sets and other data structures | Data Structures in Mathematics Math Foundations 151
In mathematics we often want to organize objects. Sets are not the only way of doing this: there are other data types that are also useful and that can be considered together with set theory. In particular when we group objects together, there are two fundamental questions that naturally a
From playlist Math Foundations
Introduction to data structures
See complete series of videos in data structures here: http://www.youtube.com/playlist?list=PL2_aWCzGMAwI3W_JlcBbtYTwiQSsOTa6P&feature=view_all In this lesson, we will introduce you to data structures as ways to store and organize data in computer. Feel free to drop your question, feedbac
From playlist Data structures

LambdaConf 2015 - The Abstract Method, In General Gershom Bazerman
“Programming is about abstraction.” But what is abstraction about? Surely not just programming. Why do we need it, why do we keep reinventing it? How do we even recognize it when we see it, across so many domains? When something is more abstract, it is not necessarily more useless, even th
From playlist LambdaConf 2015

Category Theory 1.1: Motivation and Philosophy
Motivation and philosophy
From playlist Category Theory

Josef Teichmann: An elementary proof of the reconstruction theorem
CIRM VIRTUAL EVENT Recorded during the meeting "Pathwise Stochastic Analysis and Applications" the March 09, 2021 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematician
From playlist Virtual Conference

Virtual EmberConf 2020: AST: the Secret Weapon to Transform a Codebase by Sophia Wang
AST: the Secret Weapon to Transform a Codebase by Sophia Wang Ever wonder what is metaprogramming? Ever wonder how a machine translates ember code into the websites that you interact with? Want to update your codebase to a newer syntax without going through editing every line? Curious abo
From playlist EmberConf 2020

BathRuby 2015 - A Lever for the Mind
By, Tom Stuart Abstraction is a tool that magnifies the force of the human mind. The use of abstraction to make complex ideas manageable is fundamental to our work as programmers and to human culture as a whole. That's why mathematics — the study of abstraction — is so important and powerf
From playlist BathRuby 2015

RedDotRuby 2014 - Magenta is a Lie - and Other Tales of Abstraction by Konstantin Haase
Abstraction is a fundamental approach in programming. It shapes how we solve problems, it is a defining factor in how we view the internals of software and even the world surrounding it and us. The questions of when, how and what to abstract are some of the biggest in computer science and
From playlist RedDotRuby 2014

Melanie Mitchell - Abstraction and Analogy in Artificial Intelligence - IPAM at UCLA
Recorded 15 February 2022. Melanie Mitchell of Santa Fe Institute presents "Abstraction and Analogy in Artificial Intelligence" at IPAM's Mathematics of Collective Intelligence Workshop. Abstract: Conceptual abstraction and analogy-making are key abilities underlying humans' abilities to l
From playlist Workshop: Mathematics of Collective Intelligence - Feb. 15 - 19, 2022.

Introduction to Chemical Biology 128. Lecture 11. Proteins and Amino Acid Conformations, Part 2.
UCI Chem 128 Introduction to Chemical Biology (Winter 2013) Lec 11. Introduction to Chemical Biology -- Proteins and Amino Acid Conformations -- Part 2 View the complete course: http://ocw.uci.edu/courses/chem_128_introduction_to_chemical_biology.html Instructor: Gregory Weiss, Ph.D. Lice
From playlist Chem 128: Intro to Chem Biology
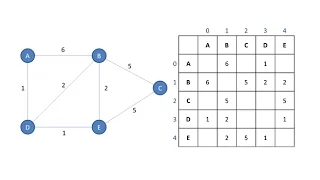
Graph Data Structure 1. Terminology and Representation (algorithms)
This is the first in a series of videos about the graph data structure. It mentions the applications of graphs, defines various terminology associated with graphs, and describes how a graph can be represented programmatically by means of adjacency lists or an adjacency matrix.
From playlist Data Structures