
Review of Linear Time Invariant Systems
http://AllSignalProcessing.com for more great signal-processing content: ad-free videos, concept/screenshot files, quizzes, MATLAB and data files. Review: systems, linear systems, time invariant systems, impulse response and convolution, linear constant-coefficient difference equations
From playlist Introduction and Background

Discrete-Time Dynamical Systems
This video shows how discrete-time dynamical systems may be induced from continuous-time systems. https://www.eigensteve.com/
From playlist Data-Driven Dynamical Systems

Introduction to Linear Time Invariant System Descriptions
http://AllSignalProcessing.com for free e-book on frequency relationships and more great signal processing content, including concept/screenshot files, quizzes, MATLAB and data files. Introduces systems and their use in signal processing; defines linearity, time invariance, and causal sys
From playlist Introduction and Background

Random Processes and Stationarity
http://AllSignalProcessing.com for more great signal-processing content: ad-free videos, concept/screenshot files, quizzes, MATLAB and data files. Introduction to describing random processes using first and second moments (mean and autocorrelation/autocovariance). Definition of a stationa
From playlist Random Signal Characterization
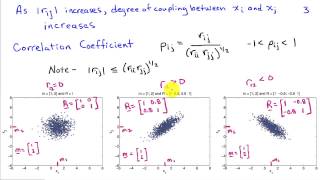
Characterization of Random, Multivariate Signals
http://AllSignalProcessing.com for more great signal-processing content: ad-free videos, concept/screenshot files, quizzes, MATLAB and data files. Multivariable (vector) probability density function representations, including the multivariate Gaussian density. The covariance matrix and in
From playlist Random Signal Characterization

Impulse Response Descriptions for Systems
http://AllSignalProcessing.com for more great signal-processing content: ad-free videos, concept/screenshot files, quizzes, MATLAB and data files. Introduces the impulse response and convolution sum for determining the output of a linear time-invariant system from the input. Defines finit
From playlist Introduction and Background

Randomness - Applied Cryptography
This video is part of an online course, Applied Cryptography. Check out the course here: https://www.udacity.com/course/cs387.
From playlist Applied Cryptography

(ML 16.7) EM for the Gaussian mixture model (part 1)
Applying EM (Expectation-Maximization) to estimate the parameters of a Gaussian mixture model. Here we use the alternate formulation presented for (unconstrained) exponential families.
From playlist Machine Learning

AQS-automata, state transition graphs, return-point by Muhittin Mungan
Program Entropy, Information and Order in Soft Matter  ORGANIZERS Bulbul Chakraborty, Pinaki Chaudhuri, Chandan Dasgupta, Marjolein Dijkstra, Smarajit Karmakar, Vijaykumar Krishnamurthy, Jorge Kurchan, Madan Rao, Srikanth Sastry and Francesco Sciortino DATE & TIME 27 August 2018 to
From playlist Entropy, Information and Order in Soft Matter

(PP 6.2) Multivariate Gaussian - examples and independence
Degenerate multivariate Gaussians. Some sketches of examples and non-examples of Gaussians. The components of a Gaussian are independent if and only if they are uncorrelated.
From playlist Probability Theory

Networks: Part 6 - Oxford Mathematics 4th Year Student Lecture
Network Science provides generic tools to model and analyse systems in a broad range of disciplines, including biology, computer science and sociology. This course (we are showing the whole course over the next few weeks) aims at providing an introduction to this interdisciplinary field o
From playlist Oxford Mathematics Student Lectures - Networks

Research talks by Nisheeth Vishno
Second Bangalore School on Population Genetics and Evolution URL: http://www.icts.res.in/program/popgen2016 DESCRIPTION: Just as evolution is central to our understanding of biology, population genetics theory provides the basic framework to comprehend evolutionary processes. Population
From playlist Second Bangalore School on Population Genetics and Evolution

Non-Hermitian Description of the Quasi-Zeno Dynamics of a Quantum Particle by Abhishek Dhar
PROGRAM NON-HERMITIAN PHYSICS (ONLINE) ORGANIZERS: Manas Kulkarni (ICTS, India) and Bhabani Prasad Mandal (Banaras Hindu University, India) DATE: 22 March 2021 to 26 March 2021 VENUE: Online Non-Hermitian Systems / Open Quantum Systems are not only of fundamental interest in physics a
From playlist Non-Hermitian Physics (ONLINE)

Order, Entropy, Information, and Compression (Lecture 3) by Dov Levine
PROGRAM ENTROPY, INFORMATION AND ORDER IN SOFT MATTER ORGANIZERS: Bulbul Chakraborty, Pinaki Chaudhuri, Chandan Dasgupta, Marjolein Dijkstra, Smarajit Karmakar, Vijaykumar Krishnamurthy, Jorge Kurchan, Madan Rao, Srikanth Sastry and Francesco Sciortino DATE: 27 August 2018 to 02 Novemb
From playlist Entropy, Information and Order in Soft Matter

Advanced asymptotics of PDEs and applications - 24 September 2018
http://www.crm.sns.it/event/424/ The aim of this workshop is to present and discuss recent advanced topics in analysis, numerical methods, and statistical physics methods for modeling and quantifying cellular functions and organization. We will focus here on recent the asymptotic of PDEs
From playlist Centro di Ricerca Matematica Ennio De Giorgi

Absorbing-State Phase Transitions by Leonardo Rolla
PROGRAM :UNIVERSALITY IN RANDOM STRUCTURES: INTERFACES, MATRICES, SANDPILES ORGANIZERS :Arvind Ayyer, Riddhipratim Basu and Manjunath Krishnapur DATE & TIME :14 January 2019 to 08 February 2019 VENUE :Madhava Lecture Hall, ICTS, Bangalore The primary focus of this program will be on the
From playlist Universality in random structures: Interfaces, Matrices, Sandpiles - 2019

Perla Sousi: Random walks on dynamical percolation
Abstract: We study the behaviour of random walk on dynamical percolation. In this model, the edges of a graph are either open or closed and refresh their status at rate μ, while at the same time a random walker moves on G at rate 1, but only along edges which are open. On the d-dimensional
From playlist Probability and Statistics

Hyperuniformity and Entropy cusps in active-absorbing phase transitions by Rahul Dandekar
DISCUSSION MEETING : 7TH INDIAN STATISTICAL PHYSICS COMMUNITY MEETING ORGANIZERS : Ranjini Bandyopadhyay, Abhishek Dhar, Kavita Jain, Rahul Pandit, Sanjib Sabhapandit, Samriddhi Sankar Ray and Prerna Sharma DATE : 19 February 2020 to 21 February 2020 VENUE : Ramanujan Lecture Hall, ICTS
From playlist 7th Indian Statistical Physics Community Meeting 2020

2020.06.25 M. Hilário - Random walks on dynamical random environments with non-uniform mixing (2/2)
In these two consecutive talks we will discuss recent results on the limiting behavior of random walks on dynamical random environments. The strength of these results depends a great deal on space-time mixing properties imposed to the environment but also on other features like the dimensi
From playlist One World Probability Seminar

Critical dynamics (Lecture - 05) by Uwe C Täuber
Bangalore School on Statistical Physics - VIII DATE: 28 June 2017 to 14 July 2017 VENUE: Ramanujan Lecture Hall, ICTS, Bengaluru This advanced level school is the eighth in the series. This is a pedagogical school, aimed at bridging the gap between masters-level courses and topics in s
From playlist Bangalore School on Statistical Physics - VIII