
Math 030 Calculus I 042915: Integrable Functions; the Definite Integral
What was arbitrary about the definition of area? Riemann Sums as generalizations of right endpoint approximation. Definition of integrable function; of definite integral. Theorem: continuous implies integrable. Example. Statement of Fundamental Theorem of Calculus II; examples.
From playlist Course 2: Calculus I

What is the constant rule of integration
👉 Learn how to evaluate the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which t
From playlist The Integral

Learn how to integrate a rational expression by simplifying first with rational powers
👉 Learn how to evaluate the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which t
From playlist The Integral

How to find the antiderivative of a quadratic polynomial
👉 Learn how to evaluate the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which t
From playlist The Integral

Find the antiderivative using u substitition with a natural logarithm
👉 Learn how to evaluate the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which t
From playlist The Integral

Find the integral given a partial and full integrand
👉 Learn how to evaluate the integral of separated functions. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral i
From playlist The Integral

How to find the antiderivative of a simple function
👉 Learn how to find the antiderivative (integral) of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integr
From playlist The Integral

Learn how to find the general solution to an antiderivative of cosine
👉 Learn how to evaluate the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which t
From playlist The Integral

Lecture 12: Lebesgue Integrable Functions, the Lebesgue Integral and the Dominated Convergence...
MIT 18.102 Introduction to Functional Analysis, Spring 2021 Instructor: Dr. Casey Rodriguez View the complete course: https://ocw.mit.edu/courses/18-102-introduction-to-functional-analysis-spring-2021/ YouTube Playlist: https://www.youtube.com/watch?v=W2pw1JWc9k4&list=PLUl4u3cNGP63micsJp_
From playlist MIT 18.102 Introduction to Functional Analysis, Spring 2021

Complex Analysis: Integral of cos(x)/(x^2+1) using Contour Integration
Today, we evaluate a very nice integral using complex analysis. Videos on integral of x*sin(x)/(x^2+1): Complex Analysis Method: https://www.youtube.com/watch?v=O0NEtZ1Yqhs&t=9s Laplace Transform Method: https://www.youtube.com/watch?v=bF7eIV5jl84
From playlist Contour Integration
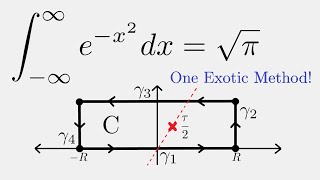
Complex Analysis: Gaussian Integral
Today, we use a very exotic contour integration methods to evaluate the Gaussian integral.
From playlist Contour Integration

Lecture 5 Lp Spaces on the real line
Lecture with Ole Christensen. Kapitler: 00:00 - Repetition; 05:00 - Introduction; 15:00 - Inequalities For Integrals; 26:00 - Support Of A Function; 31:30 - Special Continuous Functions; 34:15 - Examples;
From playlist DTU: Mathematics 4 Real Analysis | CosmoLearning.org Math

Complex Analysis: Integral of sech(ax) using Contour Integration
Today, we use a rectangular contour to evaluate the integral from -infinity to infinity of sech(ax), where a is a positive real number. Another example of the rectangular contour (Gaussian integral): https://www.youtube.com/watch?v=aw9BfO0Whic&t=1468s
From playlist Contour Integration
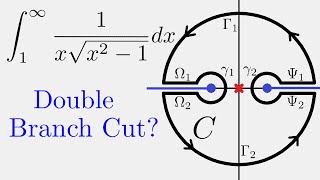
Complex Analysis: Double Keyhole Contour
Today, we use contour integration to integrate 1/(x*sqrt(x^2-1)) from 1 to infinity.
From playlist Contour Integration

Number Theory 1.4 : Analytic Continuation of the Zeta Function
In this video, I prove an analytic continuation of the Riemann Zeta function for all positive Re(z). Email : fematikaqna@gmail.com Code : https://github.com/Fematika/Animations Notes : None yet
From playlist Number Theory

MIT 18.102 Introduction to Functional Analysis, Spring 2021 Instructor: Dr. Casey Rodriguez View the complete course: https://ocw.mit.edu/courses/18-102-introduction-to-functional-analysis-spring-2021/ YouTube Playlist: https://www.youtube.com/watch?v=BYR1fXW95zY&list=PLUl4u3cNGP63micsJp_
From playlist MIT 18.102 Introduction to Functional Analysis, Spring 2021

Evaluate the partial integral given two integrans
👉 Learn how to evaluate the integral of separated functions. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral i
From playlist The Integral
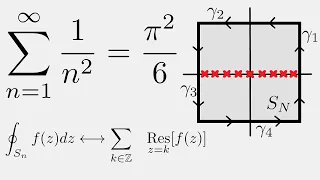
Complex Analysis: The Basel Problem
Today, we solve the Basel Problem using complex analysis! Residues at higher order poles: https://www.youtube.com/watch?v=9hdZDHkKoAM This is a long video, so here are some timestamps for each section 1:14 Chapter 1 - Motivation 5:45 Chapter 2 - Finding f(z) 13:51 Chapter 3 - Sum of the
From playlist Contour Integration

