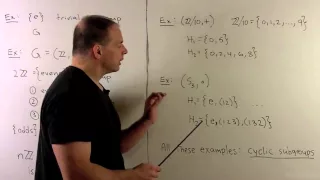
Abstract Algebra: We define the notion of a subgroup and provide various examples. We also consider cyclic subgroups and subgroups generated by subsets in a given group G. Example include A4 and D8. U.Reddit course materials available at http://ureddit.com/class/23794/intro-to-group-
From playlist Abstract Algebra

A group is (in a sense) the simplest structure in which we can do the familiar tasks associated with "algebra." First, in this video, we review the definition of a group.
From playlist Modern Algebra - Chapter 15 (groups)

Definition of a group Lesson 24
In this video we take our first look at the definition of a group. It is basically a set of elements and the operation defined on them. If this set of elements and the operation defined on them obey the properties of closure and associativity, and if one of the elements is the identity el
From playlist Abstract algebra

In this tutorial we define a subgroup and prove two theorem that help us identify a subgroup. These proofs are simple to understand. There are also two examples of subgroups.
From playlist Abstract algebra

Groups in abstract algebra examples
In this tutorial I discuss two more examples of groups. The first contains four elements and they are the four fourth roots of 1. The second contains only three elements and they are the three cube roots of 1. Under the binary operation of multiplication, these sets are in fact groups.
From playlist Abstract algebra

Simple Groups - Abstract Algebra
Simple groups are the building blocks of finite groups. After decades of hard work, mathematicians have finally classified all finite simple groups. Today we talk about why simple groups are so important, and then cover the four main classes of simple groups: cyclic groups of prime order
From playlist Abstract Algebra

Group Theory: The Center of a Group G is a Subgroup of G Proof
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Group Theory: The Center of a Group G is a Subgroup of G Proof
From playlist Abstract Algebra

Example of Group: GL(2, R) (3 of 3)
Abstract Algebra: Let G=GL(2, R) be the group of real invertible 2x2 matrices. We consider two group actions for the group GL(2, R) on itself. We interpret the results in terms of linear algebra and change of basis. We also explain how conjugacy classes of G relate to the diagonalizati
From playlist Abstract Algebra

Abstract Algebra - 3.1 Finite Groups and Subgroups: Terminology and Notation
Most of this chapter will revolve around the idea of a subgroup. However, we must begin by being able to differentiate between a finite group and infinite group. We look at some notation and definitions (order of a group, order of an element) before jumping into subgroups. Video Chapters:
From playlist Abstract Algebra - Entire Course

Division 1 | Multiplication and division | Arithmetic | Khan Academy
Courses on Khan Academy are always 100% free. Start practicing—and saving your progress—now: https://www.khanacademy.org/math/arithmetic-home/multiply-divide/division-intro/v/division-1 Introduction to division Practice this lesson yourself on KhanAcademy.org right now: https://www.khana
From playlist Multiplication and division | Arithmetic | Khan Academy

Group theory 6: normal subgroups and quotient groups
This is lecture 6 of an online mathematics course on groups theory. It defines normal subgroups and quotient groups, using the non-abelian group of order 6 as an example.
From playlist Group theory

Lie Groups and Lie Algebras: Lesson 40: SU(2) as Universal Covering Group
Lie Groups and Lie Algebras: Lesson 40: SU(2) as Universal Covering Group In this lesson we walk through the example of SO(3), SL(1,Q), and SU(2). This will prepare us for a more complex example: u(2)! Please consider supporting this channel on Patreon: https://www.patreon.com/XYLYXYLYX
From playlist Lie Groups and Lie Algebras

Group theory 24: Extra special groups
This lecture is part of an online mathematics course on group theory. It covers groups of order p^3. The non-abelian ones are examples of extra special groups, a sort of analog of the Heisenberg groups of quantum mechanics.
From playlist Group theory

Group theory 17: Finite abelian groups
This lecture is part of a mathematics course on group theory. It shows that every finitely generated abelian group is a sum of cyclic groups. Correction: At 9:22 the generators should be g, h+ng not g, g+nh
From playlist Group theory

Group theory 16: Automorphisms of cyclic groups
This lecture is part of an online mathematics course on group theory. It is mostly about the structure of the group of automorphisms of a cyclic group. As an application we classify the groups of order pq for primes p, q.
From playlist Group theory
Groups and subgroups -- Proofs
This lecture is on Introduction to Higher Mathematics (Proofs). For more see http://calculus123.com.
From playlist Proofs

Group theory 7: Semidirect products
This is lecture 7 of an online course on group theory. It covers semidirect products and uses them to classify groups of order 6.
From playlist Group theory

Group theory 19: Wreath products
This lecture is part of an online mathematics course on group theory. It describes wreath products and gives a few examples of them, such as Sylow subgroups of symmetric groups.
From playlist Group theory

Francesc Fité, Sato-Tate groups of abelian varieties of dimension up to 3
VaNTAGe seminar on April 7, 2020 License: CC-BY-NC-SA Closed captions provided by Jun Bo Lau.
From playlist The Sato-Tate conjecture for abelian varieties

This lecture is part of an online math course on group theory. We review free abelian groups, then construct free (non-abelian) groups, and show that they are given by the set of reduced words, and as a bonus find that they are residually finite.
From playlist Group theory