
Determine Limits at Infinity Involving an Exponential Function: Odd Exponent
This video explains how to determine limits at infinity analytically and using a graph.
From playlist Limits at Infinity and Special Limits

Calculus 1: Limits & Derivatives (20 of 27) Finding the Limits of a Function - Example 7
Visit http://ilectureonline.com for more math and science lectures! In this video I will calculate the limit(x approaches negative infinity) of (x^2-1)/(x^2+1). Next video in the series can be seen at: https://youtu.be/U9htc5DkFi0
From playlist CALCULUS 1 CH 1 LIMITS & DERIVATIVES

Determine Infinite Limits of a Rational Function Using a Table and Graph (Squared Denominator)
This video explains how to determine a limits and one-sided limits. The results are verified using a table and a graph.
From playlist Infinite Limits

Determine Limits at Infinity of a Sum Involving a Square Root
This video explains how to determine limits at infinity of a sum involving a square root.
From playlist Limits at Infinity and Special Limits

Anders Södergren: On Epstein’s zeta function and related random functions
Recording during the meeting "Zeta Functions" the December 02, 2019 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http:
From playlist Probability and Statistics
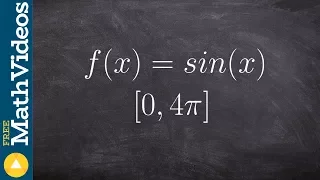
How to determine the max and min of a sine on a closed interval
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions

Determine a Limit at Infinity: Rational Function in Factored From
This video explains how to determine an infinite limit of a rational function in factored form.
From playlist Limits at Infinity and Special Limits

Nick Cook (Duke) -- Universality for the minimum modulus of random trigonometric polynomials
We consider the restriction to the unit circle of random degree-n polynomials with iid normalized coefficients (Kac polynomials). Recent work of Yakir and Zeitouni shows that for Gaussian coefficients, the minimum modulus (suitably rescaled) follows a limiting exponential distribution. We
From playlist Columbia Probability Seminar

Maximum and Minimum Values (Closed interval method)
A review of techniques for finding local and absolute extremes, including an application of the closed interval method
From playlist 241Fall13Ex3

Limit Theorems for Spatial Interacting Models by Yogeshwaran D
PROGRAM: TOPICS IN HIGH DIMENSIONAL PROBABILITY ORGANIZERS: Anirban Basak (ICTS-TIFR, India) and Riddhipratim Basu (ICTS-TIFR, India) DATE & TIME: 02 January 2023 to 13 January 2023 VENUE: Ramanujan Lecture Hall This program will focus on several interconnected themes in modern probab
From playlist TOPICS IN HIGH DIMENSIONAL PROBABILITY
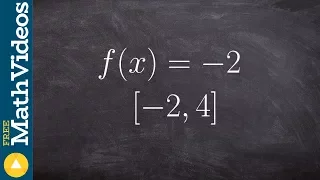
What is the max and min of a horizontal line on a closed interval
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions

FFT based spectral Ewald methods as an alternative to multipole methods – A.-K. Tornberg – ICM2018
Numerical Analysis and Scientific Computing Invited Lecture 15.5 FFT based spectral Ewald methods as an alternative to fast multipole methods Anna-Karin Tornberg Abstract: In this paper, we review a set of fast and spectrally accurate methods for rapid evaluation of three dimensional ele
From playlist Numerical Analysis and Scientific Computing

Extremal Landscape for the CbetaE Ensemble by Ofer Zeitouni
PROGRAM: TOPICS IN HIGH DIMENSIONAL PROBABILITY ORGANIZERS: Anirban Basak (ICTS-TIFR, India) and Riddhipratim Basu (ICTS-TIFR, India) DATE & TIME: 02 January 2023 to 13 January 2023 VENUE: Ramanujan Lecture Hall This program will focus on several interconnected themes in modern probab
From playlist TOPICS IN HIGH DIMENSIONAL PROBABILITY

Thermalisation, Many-Body Chaos, and Weak Solutions.. by Samriddhi Sankar Ray
PROGRAM THERMALIZATION, MANY BODY LOCALIZATION AND HYDRODYNAMICS ORGANIZERS: Dmitry Abanin, Abhishek Dhar, François Huveneers, Takahiro Sagawa, Keiji Saito, Herbert Spohn and Hal Tasaki DATE : 11 November 2019 to 29 November 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore How do is
From playlist Thermalization, Many Body Localization And Hydrodynamics 2019

Joel Kamnitzer: Categorical g-actions for modules over truncated shifted Yangians
CIRM VIRTUAL CONFERENCE Given a representation V of a reductive group G, Braverman-Finkelberg-Nakajima defined a Poisson variety called the Coulomb branch, using a convolution algebra construction. This variety comes with a natural deformation quantization, called a Coulomb branch algebr
From playlist Virtual Conference

Example of Extreme Value Theorem 3
Calculus: Find the maximum and minimum values of f(x) = |x^2 - 9| on the closed interval [-1, 4].
From playlist Calculus Pt 1: Limits and Derivatives

Thomas Mikosch : Asymptotic theory for the sample covariance matrix of a heavy-tailed [...]
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Probability and Statistics

Example of Limit at Infinity 2
Calculus: Find the limits at +/- infinity of f(x) = (x - x^{-4/3))/(x^{-2/3} - x^{-1/3}).
From playlist Calculus Pt 1: Limits and Derivatives

19. Countable-state Markov Processes
MIT 6.262 Discrete Stochastic Processes, Spring 2011 View the complete course: http://ocw.mit.edu/6-262S11 Instructor: Robert Gallager License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 6.262 Discrete Stochastic Processes, Spring 2011
