
Vertex Covers and Vertex Covering Numbers | Graph Theory
We introduce vertex covers, minimum vertex covers, and vertex covering numbers! We'll see some examples and non-examples of vertex covers, as well as minimum vertex covers and some that aren't minimum. The number of vertices in a minimum vertex cover is called the vertex covering number of
From playlist Graph Theory
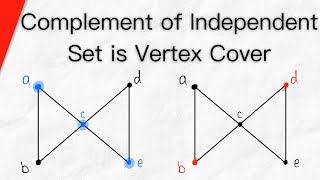
Complement of Independent Set is Vertex Cover | Graph Theory
We prove the complement of an independent vertex set is a vertex cover. This makes for an easy direct proof once we recall our definitions. An independent vertex set is a set of vertices, no two of which are adjacent. A vertex cover is a set of vertices such that every edge has at least on
From playlist Graph Theory

Raffaella Mulas - Spectral theory of hypergraphs
Hypergraphs are a generalization of graphs in which vertices are joined by edges of any size. In this talk, we generalize the graph normalized Laplace operators to the case of hypergraphs, and we discuss some properties of their spectra. We discuss the geometrical meaning of the largest an
From playlist Research Spotlight
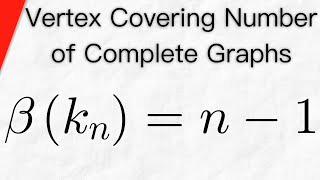
Vertex Covering Number of Complete Graphs | Graph Theory Exercises
We discuss and prove the vertex covering number of a complete graph Kn is n-1. That is, the minimum number of vertices needed to cover a complete graph is one less than its number of vertices. This is because, put simply, if we are missing at least 2 vertices in our attempted vertex cover,
From playlist Graph Theory Exercises

Emilie Purvine (5/2/21): Homology of Graphs and Hypergraphs
Graphs and hypergraphs are typically studied from a combinatorial perspective. A graph being a collection of vertices and pairwise relationships (edges) among the vertices, and a hypergraph capturing multi-way or groupwise relationships (hyperedges) among the vertices. But both of these ob
From playlist TDA: Tutte Institute & Western University - 2021
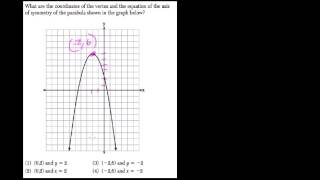
In this video we review the basic components of a parabola
From playlist Parabolas

Quadric Surface: The Hyperbolic Paraboloid
This video explains how to determine the traces of a hyperbolic paraboloid and how to graph a hyperbolic paraboloid. http://mathispower4u.yolasite.com/
From playlist Quadric, Surfaces, Cylindrical Coordinates and Spherical Coordinates

Complement of Vertex Cover is Independent Vertex Set | Graph Theory
We prove the complement of a vertex cover is an independent vertex set. Recall a vertex cover is a set of vertices covering all edges of the graph, meaning every edge has at least one end vertex in the cover. As a result, the complement of a cover cannot possible have two vertices joined b
From playlist Graph Theory
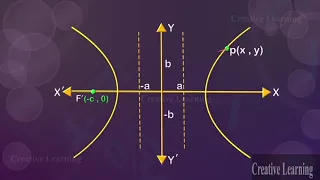
Hyperbola 3D Animation | Objective conic hyperbola | Digital Learning
Hyperbola 3D Animation In mathematics, a hyperbola is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, that are mirror images of each other an
From playlist Maths Topics

Hypergraph matchings and designs – Peter Keevash – ICM2018
Combinatorics Invited Lecture 13.10 Hypergraph matchings and designs Peter Keevash Abstract: We survey some aspects of the perfect matching problem in hypergraphs, with particular emphasis on structural characterisation of the existence problem in dense hypergraphs and the existence of d
From playlist Combinatorics

DSI | Hypergraphs and Topology for Data Science | By Emilie Purvine
Data scientists and applied mathematicians must grapple with complex data when analyzing complex systems. Analytical methods almost always represent phenomena as a much simpler level than the complex structure or dynamics inherent in systems, through either simpler measured or sampled data
From playlist DSI Virtual Seminar Series

Rainbow Matchings in Hypergraphs - Cosmin Pohoata
Computer Science/Discrete Mathematics Seminar II Topic: Rainbow Matchings in Hypergraphs Speaker: Cosmin Pohoata Affiliation: IAS - Member, School of Mathematics Date: February 14, 2023 Suppose we are given matchings M1,....,MN of size t in some r-uniform hypergraph, and let us think of
From playlist Mathematics

The Hypergraph Container Method, Partition Containers, and Algorithmic Applications - Or Zamir
Computer Science/Discrete Mathematics Seminar II Topic: The Hypergraph Container Method, Partition Containers, and Algorithmic Applications Speaker: Or Zamir Affiliation: Visitor, School of Mathematics Date: November 29, 2022 The recently-discoverd Hypergraph Container Method (Saxton an
From playlist Mathematics

More designs - P. Keevash - Workshop 1 - CEB T1 2018
Peter Keevash (Oxford) / 01.02.2018 We generalise the existence of combinatorial designs to the setting of subset sums in lattices with coordinates indexed by labelled faces of simplicial complexes. This general framework includes the problem of decomposing hypergraphs with extra edge dat
From playlist 2018 - T1 - Model Theory, Combinatorics and Valued fields

Chandra Chekuri: On element connectivity preserving graph simplification
Chandra Chekuri: On element-connectivity preserving graph simplification The notion of element-connectivity has found several important applications in network design and routing problems. We focus on a reduction step that preserves the element-connectivity due to Hind and Oellerman which
From playlist HIM Lectures 2015

Wolfram Physics I: Basic Formalism, Causal Invariance and Special Relativity
Find more information about the summer school here: https://education.wolfram.com/summer/school Stay up-to-date on this project by visiting our website: http://wolfr.am/physics Check out the announcement post: http://wolfr.am/physics-announcement Find the tools to build a universe: https:
From playlist Wolfram Summer Programs

The method of hypergraph containers – József Balogh & Robert Morris – ICM2018
Combinatorics Invited Lecture 13.6 The method of hypergraph containers József Balogh & Robert Morris Abstract: In this survey we describe a recently-developed technique for bounding the number (and controlling the typical structure) of finite objects with forbidden substructures. This te
From playlist Combinatorics

8ECM Invited Lecture: Daniela Kühn
From playlist 8ECM Invited Lectures

Finding the Equation of the Parabola Given a Point and the Vertex
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Finding the Equation of the Parabola Given a Point and the Vertex. We are also told which way the parabola opens.
From playlist Parabolas