
What is Geometric Entropy, and Does it Really Increase? - Jozsef Beck
Jozsef Beck Rutgers, The State University of New Jersey April 9, 2013 We all know Shannon's entropy of a discrete probability distribution. Physicists define entropy in thermodynamics and in statistical mechanics (there are several competing schools), and want to prove the Second Law, but
From playlist Mathematics
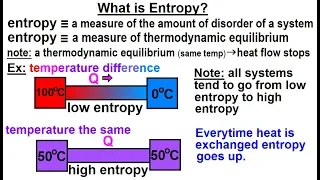
Physics - Thermodynamics 2: Ch 32.7 Thermo Potential (10 of 25) What is Entropy?
Visit http://ilectureonline.com for more math and science lectures! In this video explain and give examples of what is entropy. 1) entropy is a measure of the amount of disorder (randomness) of a system. 2) entropy is a measure of thermodynamic equilibrium. Low entropy implies heat flow t
From playlist PHYSICS 32.7 THERMODYNAMIC POTENTIALS
Entropy is often taught as a measure of how disordered or how mixed up a system is, but this definition never really sat right with me. How is "disorder" defined and why is one way of arranging things any more disordered than another? It wasn't until much later in my physics career that I
From playlist Thermal Physics/Statistical Physics

A better description of entropy
I use this stirling engine to explain entropy. Entropy is normally described as a measure of disorder but I don't think that's helpful. Here's a better description. Visit my blog here: http://stevemould.com Follow me on twitter here: http://twitter.com/moulds Buy nerdy maths things here:
From playlist Best of

Topological entropy of Hamiltonian diffeomorphisms: a persistence homology and... - Erman Cineli
Joint IAS/Princeton/Montreal/Paris/Tel-Aviv Symplectic Geometry Zoominar Topic: Topological entropy of Hamiltonian diffeomorphisms: a persistence homology and Floer theory perspective Speaker: Erman Cineli Date: February 25, 2022 In this talk I will introduce barcode entropy and discuss
From playlist Mathematics

Teach Astronomy - Entropy of the Universe
http://www.teachastronomy.com/ The entropy of the universe is a measure of its disorder or chaos. If the laws of thermodynamics apply to the universe as a whole as they do to individual objects or systems within the universe, then the fate of the universe must be to increase in entropy.
From playlist 23. The Big Bang, Inflation, and General Cosmology 2

Entropy is a very weird and misunderstood quantity. Hopefully, this video can shed some light on the "disorder" we find ourselves in... ________________________________ More videos at: http://www.youtube.com/TheScienceAsylum T-Shirts: http://scienceasylum.spreadshirt.com/ Facebook: http:/
From playlist Thermodynamics

Maxwell-Boltzmann distribution
Entropy and the Maxwell-Boltzmann velocity distribution. Also discusses why this is different than the Bose-Einstein and Fermi-Dirac energy distributions for quantum particles. My Patreon page is at https://www.patreon.com/EugeneK 00:00 Maxwell-Boltzmann distribution 02:45 Higher Temper
From playlist Physics

The lecture was held within the framework of the Hausdorff Trimester Program "Dynamics: Topology and Numbers": Conference on “Transfer operators in number theory and quantum chaos” Abstract: In many classical compact settings, entropy is upper semicontinuous, i.e., given a con
From playlist Conference: Transfer operators in number theory and quantum chaos

Reeb orbits that force topological entropy - Abror Pirnapasov
IAS/PU-Montreal-Paris-Tel-Aviv Symplectic Geometry Topic: Reeb orbits that force topological entropy Speaker: Abror Pirnapasov Affiliation: Ruhr-Universität Bochum Date: June 4, 2020 For more video please visit http://video.ias.edu
From playlist Mathematics

David Burguet: Some new dynamical applications of smooth parametrizations for C∞ systems - lecture 3
Smooth parametrizations of semi-algebraic sets were introduced by Yomdin in order to bound the local volume growth in his proof of Shub’s entropy conjecture for C∞ maps. In this minicourse we will present some refinement of Yomdin’s theory which allows us to also control the distortion. We
From playlist Dynamical Systems and Ordinary Differential Equations

Rocío González Díaz (3/16/22): Persistent entropy, a tool for topologically summarizing data.
Title: Introducing persistent entropy, a tool for topologically summarizing data. Properties and applications. Abstract: In this talk, I will introduce an entropy-based summarization of persistence barcodes. We will study some of its properties, including its stability to small perturb
From playlist AATRN 2022

Equidistribution of Measures with High Entropy for General Surface Diffeomorphisms by Omri Sarig
PROGRAM : ERGODIC THEORY AND DYNAMICAL SYSTEMS (HYBRID) ORGANIZERS : C. S. Aravinda (TIFR-CAM, Bengaluru), Anish Ghosh (TIFR, Mumbai) and Riddhi Shah (JNU, New Delhi) DATE : 05 December 2022 to 16 December 2022 VENUE : Ramanujan Lecture Hall and Online The programme will have an emphasis
From playlist Ergodic Theory and Dynamical Systems 2022

Tom Leinster : The categorical origins of entropy
Recording during the thematic meeting : "Geometrical and Topological Structures of Information" the August 29, 2017 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent
From playlist Geometry

Vaughn Climenhaga: Beyond Bowen specification property - lecture 1
Rufus Bowen introduced the specification property for uniformly hyperbolic dynamical systems and used it to establish uniqueness of equilibrium states, including the measure of maximal entropy. After reviewing Bowen's argument, we will present our recent work on extending Bowen's approach
From playlist Dynamical Systems and Ordinary Differential Equations

Hofer's Geometry and Braid Stability - Marcelo Alves
Joint IAS/Princeton/Montreal/Paris/Tel-Aviv Symplectic Geometry Zoominar Topic: Hofer's Geometry and Braid Stability Speakere: Marcelo Alves Affiliation: University of Antwerp Date: December 16, 2022 The Hofer’s metric dH is a remarkable bi-invariant metric on the group of Hamiltonian di
From playlist Mathematics

MagLab Theory Winter School 2018: Ryu Shinsei: Quantum Entangle in Conformal & Topological 2
The National MagLab held it's sixth Theory Winter School in Tallahassee, FL from January 8th - 13th, 2018.
From playlist 2018 Theory Winter School

Bourbaki - 16/01/2016 - 1/4 - Damien GABORIAU
Damien GABORIAU — Entropie sofique [d'après L. Bowen, D. Kerr et H. Li] L’entropie fut introduite en systèmes dynamiques par A. Kolmogorov. Initialement focalisée sur les itérations d’une transformation préservant une mesure finie, la notion fut peu à peu généralisée, jusqu’à embrasser l
From playlist Bourbaki - 16 janvier 2016

Is ENTROPY Really a "Measure of Disorder"? Physics of Entropy EXPLAINED and MADE EASY
This is how I personally wrapped my head around the idea of entropy! I found the statistical mechanics explanation much easier to grasp than the thermodynamics (original) one. Hey everyone, I'm back with another video, and this one has been highly requested! I really enjoy making videos a
From playlist Thermodynamics by Parth G