Martin Schweizer: Some stochastic Fubini theorems
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Analysis and its Applications

Functional Analysis Lecture 22 2014 04 15 L^p boundedness of Singular Integrals, ct’d.
(Continuing the proof) 1-atoms. Hormander condition. Control on atoms. Going for the weak-type estimate.
From playlist Course 9: Basic Functional and Harmonic Analysis

Alessio Figalli, Fields medallist 2018 - International Meeting - 16 January 2019
https://www.sns.it/it/evento/alessio-figalli-fields-medallist-2018 Alessio Figalli, Fields medallist 2018 International Meeting This event gathers mathematicians that had a major role in Figalli’s career, either by inspiring and guiding him during his early stage, or by collaborating wit
From playlist Centro di Ricerca Matematica Ennio De Giorgi

Alessandra Sarti, Old and new on the symmetry groups of K3 surfaces
VaNTAGe Seminar, Feb 9, 2021
From playlist Arithmetic of K3 Surfaces

Functional Analysis Lecture 14 2014 03 11 BMO is the dual of H^1; Distributions
Showing that integration against a BMO function is a bounded linear functional on Hardy space (using the atomic decomposition): case of an L^infinity function; case of general BMO function. Proof of converse statement. Distributions. Set D of infinitely differentiable functions of compa
From playlist Course 9: Basic Functional and Harmonic Analysis

Functional Analysis Lecture 05 2014 02 04 Hahn-Banach Theorem and Applications
Statement of Hahn-Banach; proof; application to dual linear transformations; L^1 is not the dual of L^infinity.
From playlist Course 9: Basic Functional and Harmonic Analysis

Giuseppe Mingione - 23 September 2016
Mingione, Giuseppe "Recent progresses in nonlinear potential theory"
From playlist A Mathematical Tribute to Ennio De Giorgi
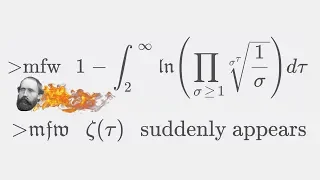
A CRAZY INTEGRAL! Evaluating one Zeta Boi
Help me create more free content! =) https://www.patreon.com/mathable Merch :v - https://teespring.com/de/stores/papaflammy Today we are going to evaluate an integral which has been proposed as a challenge on my subreddit! It includes roots, infinite sums and products, the riemann Zeta f
From playlist Integrals

Learn to evaluate the integral with functions as bounds
👉 Learn about the fundamental theorem of calculus. The fundamental theorem of calculus is a theorem that connects the concept of differentiation with the concept of integration. The theorem is basically saying that the differentiation of the integral of a function yields the original funct
From playlist Evaluate Using The Second Fundamental Theorem of Calculus

Daniele Agostini - Curves and theta functions: algebra, geometry & physics
Riemann’s theta function is a central object throughout mathematics, from algebraic geometry to number theory, and from mathematical physics to statistics and cryptography. One of my long term projects is to develop a program to study and connect the various aspects - geometric, computatio
From playlist Research Spotlight

Applied Probability: Birth processes (part 2) - Oxford Mathematics 3rd Year Student Lecture
In the second of 2 lectures from her 3rd Year Undergraduate course (you can watch the first on this channel), Christina Goldschmidt discusses Birth processes. Birth processes are some of the simplest continuous-time Markov chains: they model the size of a population which can only increas
From playlist Oxford Mathematics Student Lectures - Probability

The Niyogi-Smale-Weinberger Theorem & its relatives [Josué Tonelli Cueto]
In TDA, we compute the topology of an object by getting a finite sample of this object and fattening the points of this sample. Here, some question arises: When is a sample good enough? When does a fattening of a sample allow us to capture the topology of the object we study? The Niyogi-Sm
From playlist Tutorial-a-thon 2021 Spring

Number Theory 3.1: Analytic Continuation of the Xi/Zeta Function (ACZ 1/2)
In this video, I will prove the analytic continuation of the xi function, which will lead into the continuation of the Riemann Zeta Function. Translate This Video : http://www.youtube.com/timedtext_video?v=epnPu9mx738&ref=share Notes : None yet Patreon : https://www.patreon.com/user?u=164
From playlist Number Theory

Guido Emilio Tonelli, 9th FCC-ee Physics Workshop - Tuesday, 3 February 2015
The FCC design study General presentations about the design study, the machines and the physics of FCC-hh and FCC-ee, with synergies and complementarities. Aims at a wide audience to make the project better known in Italy. FCC-hh physics Speaker: Guido Emilio Tonelli
From playlist 9th FCC-ee Physics Workshop - 3-5 February 2015

Evaluate the integral with e as the lower bound
👉 Learn about the fundamental theorem of calculus. The fundamental theorem of calculus is a theorem that connects the concept of differentiation with the concept of integration. The theorem is basically saying that the differentiation of the integral of a function yields the original funct
From playlist Evaluate Using The Second Fundamental Theorem of Calculus

Functional Analysis Lecture 25 2014 04 29 More applications of the Baire Category Theorem
Recall: basic concepts in Fourier Series (Fourier coefficients, partial sums, Dirichlet kernel). Application: continuous functions whose Fourier series diverge on a dense set are generic. Application: Open Mapping Theorem (any continuous, surjective linear transformation between Banach
From playlist Course 9: Basic Functional and Harmonic Analysis

Subderivatives and Lagrange's Approach to Taylor Expansions | Algebraic Calculus Two | Wild Egg
The great Italian /French mathematician J. L. Lagrange had a vision of analysis following on from the algebraic approach of Euler (and even of Newton before them both). However Lagrange's insights have unfortunately been largely lost in the modern treatment of the subject. It is time to re
From playlist Algebraic Calculus Two

Calculus, heat flow and curvature-dimension in metric measure spaces – Luigi Ambrosio – ICM2018
Plenary Lecture 7 Calculus, heat flow and curvature-dimension bounds in metric measure spaces Luigi Ambrosio Abstract: The theory of curvature-dimension bounds for metric measure structure has several motivations: the study of functional and geometric inequalities in structures which are
From playlist Plenary Lectures

Math 139 Fourier Analysis Lecture 37: Dirichlet's theorem pt.4
Defining the logarithm of an L-function. Second reduction of the problem: proving non-vanishing of the L-function. Case of complex Dirichlet characters.
From playlist Course 8: Fourier Analysis

Non commutative K3 surfaces, with application to Hyperkäler... (Lecture 1) by Emanuele Macri
DISCUSSION MEETING: MODULI OF BUNDLES AND RELATED STRUCTURES ORGANIZERS : Rukmini Dey and Pranav Pandit DATE: 10 February 2020 to 14 February 2020 VENUE: Ramanujan Lecture Hall, ICTS, Bangalore Background: At its core, much of mathematics is concerned with the problem of classifying
From playlist Moduli Of Bundles And Related Structures 2020