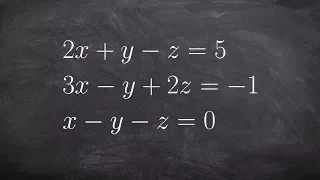
Systems of equations three variables three equations
👉Learn how to solve a system of three linear systems. A system of equations is a set of equations which are to be solved simultaneously. A linear equation is an equation whose graph is a straight line. The solution to a system of equations is a set of unique values of the variables for wh
From playlist 3 Examples: Solve a System of Three Equations

System of Equations with Three Equations and Three Variables
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys System of Equations with Three Equations and Three Variables
From playlist Systems of Equations

Waves 2_11 General Differential Equation of Waves
Developing a general differential equation for any wave.
From playlist Physics - Waves

Waves 2_10 General Differential Equation of Waves
Developing the general differential equation for any wave.
From playlist Physics - Waves

The Definition of a Linear Equation in Two Variables
This video defines a linear equation in to variables and provides examples of the different forms of linear equations. http://mathispower4u.com
From playlist The Coordinate Plane, Plotting Points, and Solutions to Linear Equations in Two Variables

Ex: Write a System of Equations as a Matrix Equation (3x3)
This video explains how to write a matrix equation for a system of three equations with three unknowns. http://mathispower4u.com
From playlist Matrix Equations
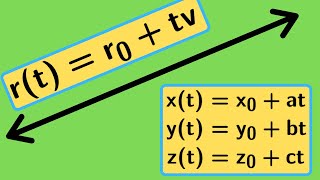
Multivariable Calculus | Three equations for a line.
We present three equations that represent the same line in three dimensions: the vector equation, the parametric equations, and the symmetric equation. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Lines and Planes in Three Dimensions

Waves 2_12 General Differential Equation of Waves
Developing a general differential equation for any wave.
From playlist Physics - Waves

How to solve a system of equations with three variables
👉Learn how to solve a system of three linear systems. A system of equations is a set of equations which are to be solved simultaneously. A linear equation is an equation whose graph is a straight line. The solution to a system of equations is a set of unique values of the variables for wh
From playlist 3 Examples: Solve a System of Three Equations

Inverse Problems Involving Non-linear Hyperbolic Equations (Lecture - 1) by Matti Lassas
DISCUSSION MEETING WORKSHOP ON INVERSE PROBLEMS AND RELATED TOPICS (ONLINE) ORGANIZERS: Rakesh (University of Delaware, USA) and Venkateswaran P Krishnan (TIFR-CAM, India) DATE: 25 October 2021 to 29 October 2021 VENUE: Online This week-long program will consist of several lectures by
From playlist Workshop on Inverse Problems and Related Topics (Online)

Standing Waves on a String, Fundamental Frequency, Harmonics, Overtones, Nodes, Antinodes, Physics
This Physics video tutorial explains the concept of standing waves on a string. It shows you how to calculate the fundamental frequency and any additional harmonics or overtones. In addition, it shows you how to identify and count the number of nodes and antinodes on a standing wave give
From playlist New Physics Video Playlist

The equation of a wave | Physics | Khan Academy
In this video David shows how to determine the equation of a wave, how that equation works, and what the equation represents. Created by David SantoPietro. Watch the next lesson: https://www.khanacademy.org/science/physics/mechanical-waves-and-sound/sound-topic/v/production-of-sound?utm_s
From playlist Oscillations and mechanical waves | Physics | Khan Academy
Lec 13 | MIT 2.71 Optics, Spring 2009
Lecture 13: 3D wave phenomena; introduction to electromagnetics Instructor: George Barbastathis, Colin Sheppard, Se Baek Oh View the complete course: http://ocw.mit.edu/2-71S09 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http:/
From playlist MIT 2.71 Optics, Spring 2009

Jérémie Szeftel The resolution of the bounded L2 curvature conjecture in General Relativity (Part 1)
In order to control locally a space-time which satisfies the Einstein equations, what are the minimal assumptions one should make on its curvature tensor? The bounded L2 curvature conjecture roughly asserts that one should only need L2 bounds of the curvature tensor on a given space-like
From playlist Ecole d'été 2014 - Analyse asymptotique en relativité générale

Your Daily Equation #13: Generalized Schrödinger Equation
Episode 13 #YourDailyEquation: Where do quantum waves do their waving? For a single particle, our three dimensional space provides a natural answer. But what if we consider more than one particle? In this episode of Your Daily Equation, this question takes us into higher dimensional spaces
From playlist Your Daily Equation with Brian Greene

Gunther Uhlmann - Seeing Through Space-Time - IPAM at UCLA
Recorded 15 September 2021. Gunther Uhlmann of the University of Washington presents "Seeing Through Space-Time" at IPAM's Mathematical and Computational Challenges in the Era of Gravitational Wave Astronomy Tutorial Abstract: The first inverse problem we will consider is whether we can de
From playlist Tutorials: Math & Computational Challenges in the Era of Gravitational Wave Astronomy

Climate Science, Waves, and PDE's for the Tropics ( 1 ) - Andrew J. Majda
Lecture 1: Climate Science, Waves, and PDE's for the Tropics: Observations, Theory, and Numerics Abstract: Geophysical flows are a rich source of novel problems for applied mathematics and the contemporary theory of partial differential equations. The reason for this is that many physical
From playlist Mathematical Perspectives on Clouds, Climate, and Tropical Meteorology

Lecture 18 (CEM) -- Plane Wave Expansion Method
This lecture steps the student through the formulation and implementation of the plane wave expansion method. It describes how to construct electromagnetic band diagrams and isofrequency contours. As bonus sections, it describes how to handle band crossing, how to implement the efficient
From playlist UT El Paso: CEM Lectures | CosmoLearning.org Electrical Engineering

Matti Lassas - Inverse problems for Einstein’s equations and other non-linear hyperbolic equations
Recorded 29 October 2021. Matti Lassas of the University of Helsinki presents "Inverse problems for Einstein’s equations and other non-linear hyperbolic equations" at IPAM's Workshop II: Mathematical and Numerical Aspects of Gravitation. Abstract: We consider inverse problems for non-linea
From playlist Workshop: Mathematical and Numerical Aspects of Gravitation
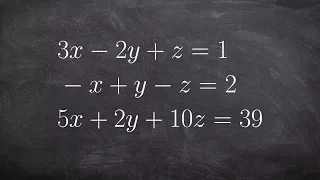
Learn to solve a system of three equations
👉Learn how to solve a system of three linear systems. A system of equations is a set of equations which are to be solved simultaneously. A linear equation is an equation whose graph is a straight line. The solution to a system of equations is a set of unique values of the variables for wh
From playlist 3 Examples: Solve a System of Three Equations