
New Methods in Finsler Geometry - 22 May 2018
http://www.crm.sns.it/event/415 Centro di Ricerca Matematica Ennio De Giorgi The workshop has limited funds to support lodging (and in very exceptional cases, travel) costs of some participants, with priority given to young researchers. When you register, you will have the possibility to
From playlist Centro di Ricerca Matematica Ennio De Giorgi

New Methods in Finsler Geometry - 23 May 2018
http://www.crm.sns.it/event/415 Centro di Ricerca Matematica Ennio De Giorgi The workshop has limited funds to support lodging (and in very exceptional cases, travel) costs of some participants, with priority given to young researchers. When you register, you will have the possibility to
From playlist Centro di Ricerca Matematica Ennio De Giorgi

Paraboloids and associated quadratic forms | Differential Geometry 23 | NJ Wildberger
Paraboloids are going to play a special role in our understanding of curvature. The idea is that we are going to locally approximate a surface S near a point by a normal paraboloid---one that shares the same tangent plane, but has an axis which is perpendicular to that tangent plane. It w
From playlist Differential Geometry

Tangent Tangent Angle Theorems - Circles & Arc Measures - Geometry
This geometry video tutorial provides a basic introduction into tangent tangent angle theorems as it relates to circles and arc measures. The sum of the minor arc and the tangent tangent angle is supplementary. The two angles add up to 180. This tutorial contains plenty of examples and
From playlist Geometry Video Playlist
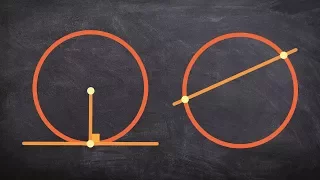
What is the difference between a secant and tangent line
Learn the essential definitions of the parts of a circle. A secant line to a circle is a line that crosses exactly two points on the circle while a tangent line to a circle is a line that touches exactly one point on the circle. A chord is a line that has its two endpoints on the circle.
From playlist Essential Definitions for Circles #Circles
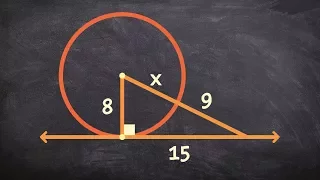
How to determine the value of x using the definition of a tangent line to a circle
Learn how to solve problems with tangent line. A tangent line to a circle is a line that touches the circle at exactly one point. The tangent line to a circle makes a right angle with the radius of the circle at the point of its tangency. Thus, to solve for any missing value involving the
From playlist Circles

Robert Bryant, A visit to the Finsler world
Robert Bryant, Duke University, USA A visit to the Finsler world
From playlist Conférence en l'honneur de Jean-Pierre Bourguignon
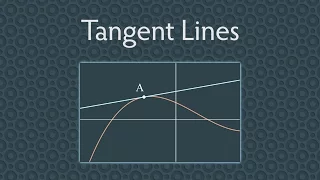
The Tangent Line and the Derivative (Calculus)
In calculus, you’ll often hear “The derivative is the slope of the tangent line.” But what is a tangent line? The definition is trickier than you might think. Tangent lines are important because they are the best way to approximate a curve using a line. We can then use the slope of the
From playlist Calculus

What is the definition of a tangent line to a circle
Learn the essential definitions of the parts of a circle. A secant line to a circle is a line that crosses exactly two points on the circle while a tangent line to a circle is a line that touches exactly one point on the circle. A chord is a line that has its two endpoints on the circle.
From playlist Essential Definitions for Circles #Circles

Meusnier, Monge and Dupin III | Differential Geometry 33 | NJ Wildberger
We look at some of the work of Charles Dupin, a French naval engineer and student of Monge. He made some lovely discoveries about triply orthogonal surfaces and lines of curvatures, for example confocal families of ellipses and hyperbolas. He studied conjugate directions on surfaces (going
From playlist Differential Geometry

How do two tangents line compare if they run through the same point
Learn how to solve problems with tangent line. A tangent line to a circle is a line that touches the circle at exactly one point. The tangent line to a circle makes a right angle with the radius of the circle at the point of its tangency. Thus, to solve for any missing value involving the
From playlist Circles

Veronica Miro Pina - Chromosome painting
We consider a simple population genetics model with recombination. We assume that at time 0, all individuals of a haploid population have their unique chromosome painted in a distinct color. At rare birth events, due to recombination (modeled as a single crossing-over), the chromosome of t
From playlist Les probabilités de demain 2017

Tangents to Circles: 2 Dynamic Illustrations without Words
GeoGebra Link: https://www.geogebra.org/m/nPWzTnAq
From playlist Geometry: Dynamic Interactives!

Bertrand Maury: Mathematics behind some phenomena in crowd motion: Stop and Go waves and...
Abstract: This minicourse aims at providing tentative explanations of some specific phenomena observed in the motion of crowds, or more generally collections of living entities. The first lecture shall focus on the so-called Stop and Go Waves, which sometimes spontaneously emerge and persi
From playlist Mathematical Physics

Pierre-Emmanuel Jabin: A new commutator method for averaging lemmas - lecture 2
CIRM HYBRID EVENT Recorded during the meeting "Scaling Limits from Microscopic to Macroscopic Physics" the January 19, 2021 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwid
From playlist Virtual Conference

Tangent Properties - Circle Geometry (Tangents from an external point are equal)
More resources available at www.misterwootube.com
From playlist Circle Geometry
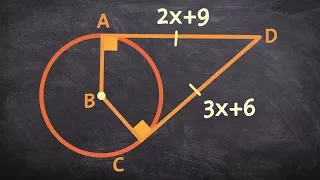
Determine the value of x when given two tangent lines to a circle
Learn how to solve problems with tangent line. A tangent line to a circle is a line that touches the circle at exactly one point. The tangent line to a circle makes a right angle with the radius of the circle at the point of its tangency. Thus, to solve for any missing value involving the
From playlist Circles

New Methods in Finsler Geometry - 25 May 2018
http://www.crm.sns.it/event/415 Centro di Ricerca Matematica Ennio De Giorgi The workshop has limited funds to support lodging (and in very exceptional cases, travel) costs of some participants, with priority given to young researchers. When you register, you will have the possibility to
From playlist Centro di Ricerca Matematica Ennio De Giorgi
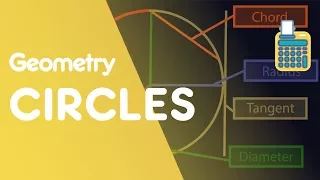
Circle Terminology - Radius Diameter Sector Segment Chord Arc Tangent | Geometry | Math | FuseSchool
DESCRIPTION: There are some key words we need to know for circles: radius, circumference, diameter, sector, segment, tangent, chord and arc. In this video we discover what they all mean. The radius is the distance from the centre of a circle to a point on the circle. A diameter is the dist
From playlist MATHS: Geometry & Measures
