
Metrizable universal minimal flows and Ramsey theory - T. Tsankov - Workshop 1 - CEB T1 2018
Todor Tsankov (Université Paris Diderot) / 01.02.2018 The connection between Ramsey theory and topological dynamics goes back at least to Furstenberg who used dynamical systems of the group of integers to derive a new proof of Van Der Waerden’s theorem. More recently, Kechris, Pestov, and
From playlist 2018 - T1 - Model Theory, Combinatorics and Valued fields

Ramsey theory is based on Ramsey's theorem, because without it, there would be no Ramsey numbers, since they are not well-defined. This is part 2 of the trilogy of the Ramsey numbers. Useful link: https://en.wikipedia.org/wiki/Ramsey%27s_theorem#2-colour_case Other than commenting on the
From playlist Ramsey trilogy

Ramsey theorems for classes of structures with (...) - J. Hubička - Workshop 1 - CEB T1 2018
Jan Hubička (Charles U) / 02.02.2018 Ramsey theorems for classes of structures with functions and relations We discuss a generalization of Nešetřil-Rődl theorem for free amalgamation classes of structures in a language containing both relations and partial functions. Then we further stre
From playlist 2018 - T1 - Model Theory, Combinatorics and Valued fields

Advances on Ramsey numbers - Jacob Fox
https://www.math.ias.edu/seminars/abstract?event=83564
From playlist Computer Science/Discrete Mathematics

Using nonstandard natural numbers in Ramsey Theory - M. Di Nasso - Workshop 1 - CEB T1 2018
Mauro Di Nasso (Pisa) / 01.02.2018 In Ramsey Theory, ultrafilters often play an instrumental role. By means of nonstandard models, one can reduce those third-order objects (ultrafilters are sets of sets of natural numbers) to simple points. In this talk we present a nonstandard technique
From playlist 2018 - T1 - Model Theory, Combinatorics and Valued fields

23 Algebraic system isomorphism
Isomorphic algebraic systems are systems in which there is a mapping from one to the other that is a one-to-one correspondence, with all relations and operations preserved in the correspondence.
From playlist Abstract algebra

An introduction to the Tropical calculus | Data Structures in Mathematics Math Foundations 158
We give a short informal introduction to the Tropical calculus, which for us is a novel way of working with the algebra of sets and multisets. This involves defining rather unusual notions of addition and multiplication-- coming from union and addition respectively. **********************
From playlist Math Foundations

Automorphism groups and Ramsey properties of sparse graphs - D. Evans - Workshop 1 - CEB T1 2018
David Evans (Imperial) / 30.01.2018 An infinite graph is sparse if there is a positive integer k such that for every finite subgraph, the number of edges is bounded above by k times the number of vertices. Such graphs arise in model theory via Hrushovskis predimension constructions. In jo
From playlist 2018 - T1 - Model Theory, Combinatorics and Valued fields

Natasha Dobrinen: Borel sets of Rado graphs are Ramsey
The Galvin-Prikry theorem states that Borel partitions of the Baire space are Ramsey. Thus, given any Borel subset $\chi$ of the Baire space and an infinite set $N$, there is an infinite subset $M$ of $N$ such that $\left [M \right ]^{\omega }$ is either contained in $\chi$ or disjoint fr
From playlist Combinatorics
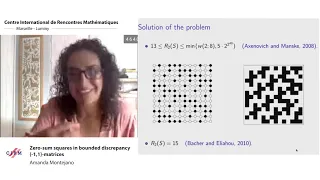
Amanda Montejano: Zero-sum squares in bounded discrepancy {-1,1}-matrices
A square in a matrix $\mathcal M =(a_{ij})$ is a 2X2 sub-matrix of $\mathcal M$ with entries $a_{ij}, a_{i+s,j}, ai,j+s, a_{i+s,j+s}$s for some $s\geq 1$. An Erickson matrix is a square binary matrix that contains no squares with constant entries. In [Eri96], Erickson asked for the maximum
From playlist Virtual Conference

Category Theory 3.1: Examples of categories, orders, monoids
Examples of categories, orders, monoids.
From playlist Category Theory

The absorption method, and an application to an old Ramsey problem - Matija Bucic
Computer Science/Discrete Mathematics Seminar II Topic: The absorption method, and an application to an old Ramsey problem Speaker: Matija Bucic Affiliation: Veblen Research Instructor, School of Mathematics Date: March 29, 2022 The absorption method is a very simple yet surprisingly pow
From playlist Mathematics

Ramsey classes and sparsity for finite models - J. Nešetřil - Workshop 1 - CEB T1 2018
Jaroslav Nešetřil (Prague) / 31.01.2018 In the talk we relate two notions in the title particularly in the context of sparse dense dichotomy (nowhere and somewhere dense classes and stability) and Ramsey classes of finite models in the context of the characterisation programme. A joint wo
From playlist 2018 - T1 - Model Theory, Combinatorics and Valued fields
This video is about some of the basic properties of Ramsey numbers.
From playlist Basics: Graph Theory

The origin of countless conspiracy theories - PatrickJMT
View full lesson: http://ed.ted.com/lessons/the-origin-of-countless-conspiracy-theories-patrickjmt Check out PatrickJMT's YouTube channel here: https://www.youtube.com/user/patrickJMT Why can we find geometric shapes in the night sky? How can we know that at least two people in London ha
From playlist New TED-Ed Originals

1. A bridge between graph theory and additive combinatorics
MIT 18.217 Graph Theory and Additive Combinatorics, Fall 2019 Instructor: Yufei Zhao View the complete course: https://ocw.mit.edu/18-217F19 YouTube Playlist: https://www.youtube.com/playlist?list=PLUl4u3cNGP62qauV_CpT1zKaGG_Vj5igX In an unsuccessful attempt to prove Fermat's last theorem
From playlist MIT 18.217 Graph Theory and Additive Combinatorics, Fall 2019

Vitaly Bergelson: Mutually enriching connections between ergodic theory and combinatorics - part 8
Abstract : * The early results of Ramsey theory : Hilbert's irreducibility theorem, Dickson-Schur work on Fermat's equation over finite fields, van der Waerden's theorem, Ramsey's theoremand its rediscovery by Erdos and Szekeres. * Three main principles of Ramsey theory : First principl
From playlist Jean-Morlet Chair - Lemanczyk/Ferenczi

Dependent random choice - Jacob Fox
Marston Morse Lectures Topic: Dependent random choice Speaker: Jacob Fox, Stanford University Date: October 26, 2016 For more videos, visit http://video.ias.edu
From playlist Mathematics

Bruno Klingler - 4/4 Tame Geometry and Hodge Theory
Hodge theory, as developed by Deligne and Griffiths, is the main tool for analyzing the geometry and arithmetic of complex algebraic varieties. It is an essential fact that at heart, Hodge theory is NOT algebraic. On the other hand, according to both the Hodge conjecture and the Grothendie
From playlist Bruno Klingler - Tame Geometry and Hodge Theory

Rhapsody on Ramsey numbers (and aliens?)
Why are aliens involved in this graph theory problem? This video trilogy will investigate deep into Ramsey's theory, ultimately showing R(4,4)=18. Although this field of graph theory is pretty famous and possibly covered by many Youtube channels, this more-than-20-minute journey Other th
From playlist Ramsey trilogy