
A path integral approach to entanglement and non-equilibrium dynamics by Krishnendu Sengupta
PROGRAM THERMALIZATION, MANY BODY LOCALIZATION AND HYDRODYNAMICS ORGANIZERS: Dmitry Abanin, Abhishek Dhar, François Huveneers, Takahiro Sagawa, Keiji Saito, Herbert Spohn and Hal Tasaki DATE : 11 November 2019 to 29 November 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore How do is
From playlist Thermalization, Many Body Localization And Hydrodynamics 2019

Dispersion in confined and fluctuating systems by David Dean
DISCUSSION MEETING : STATISTICAL PHYSICS OF COMPLEX SYSTEMS ORGANIZERS : Sumedha (NISER, India), Abhishek Dhar (ICTS-TIFR, India), Satya Majumdar (University of Paris-Saclay, France), R Rajesh (IMSc, India), Sanjib Sabhapandit (RRI, India) and Tridib Sadhu (TIFR, India) DATE : 19 December
From playlist Statistical Physics of Complex Systems - 2022

Steve Fitzgerald - Path integral formulation of stochastic processes... - IPAM at UCLA
Recorded 30 March 2023. Steve Fitzgerald of the University of Leeds presents "Path integral formulation of stochastic processes: non-equilibrium reaction pathways, hyperdynamics, and enhanced sampling" at IPAM's Increasing the Length, Time, and Accuracy of Materials Modeling Using Exascale
From playlist 2023 Increasing the Length, Time, and Accuracy of Materials Modeling Using Exascale Computing

Martin Hairer Colloquium Talk: Taming Infinities
SMRI-MATRIX Symposium with Martin Hairer 3 February 2021: Colloquium talk Title: Taming infinities Abstract: Some physical and mathematical theories have the unfortunate feature that if one takes them at face value, many quantities of interest appear to be infinite! What's worse, this
From playlist Symposium with Martin Hairer

What is an integral and it's parts
👉 Learn about integration. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which the upper and the lower li
From playlist The Integral

Find the integral with a given condition
👉 Learn how to find the particular solution to the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as indefinite integral or as a definite integral. A definite integral is an
From playlist The Integral

Integrate cosine using u substitution
👉 Learn how to evaluate the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which t
From playlist The Integral

Apply u substitution to a polynomial
👉 Learn how to evaluate the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which t
From playlist The Integral

What is the constant rule of integration
👉 Learn how to evaluate the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which t
From playlist The Integral

Determine the paticular solution of integration
👉 Learn how to find the particular solution to the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as indefinite integral or as a definite integral. A definite integral is an
From playlist The Integral
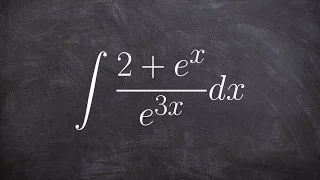
How to integrate with e in the numerator and denominator
👉 Learn how to evaluate the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which t
From playlist The Integral
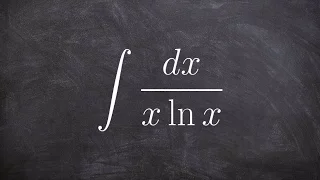
How to u substitution to natural logarithms
👉 Learn how to evaluate the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which t
From playlist The Integral

How to integrate when there is a radical in the denominator
👉 Learn how to evaluate the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which t
From playlist The Integral

MATH2018 Lecture 4.1 Double Integrals
Double integration extends the concepts of regular integration to functions of more than one variable. Instead of finding the area under a curve, we will be calculating the volume under a surface.
From playlist MATH2018 Engineering Mathematics 2D

Lecture 12: Lebesgue Integrable Functions, the Lebesgue Integral and the Dominated Convergence...
MIT 18.102 Introduction to Functional Analysis, Spring 2021 Instructor: Dr. Casey Rodriguez View the complete course: https://ocw.mit.edu/courses/18-102-introduction-to-functional-analysis-spring-2021/ YouTube Playlist: https://www.youtube.com/watch?v=W2pw1JWc9k4&list=PLUl4u3cNGP63micsJp_
From playlist MIT 18.102 Introduction to Functional Analysis, Spring 2021

All calculus integration techniques: Integration by parts, DI method, reverse power rule, u-substitution, trigonometric substitution, integration by substitution, integration by partial fraction decomposition, trigonometric integrals, and more. An extreme calculus tutorial by @blackpenredp
From playlist 100 Everything
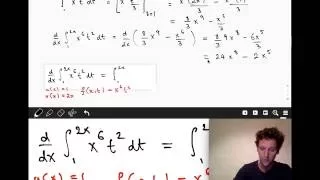
MATH2018 Lecture 1.4 Liebniz' Rule
Liebniz' Rule tells us how to deal with the case when we differentiate an integral of a function of more than one variable.
From playlist MATH2018 Engineering Mathematics 2D

Worldwide Calculus: Improper Integrals
Lecture on 'Improper Integrals' from 'Worldwide Integral Calculus' and 'Worldwide AP Calculus'. For more lecture videos and $10 digital textbooks, visit www.centerofmath.org.
From playlist Continuous Sums: the Definite Integral

Worldwide Calculus: Integration in R²
Lecture on 'Integration in R²' from 'Worldwide Multivariable Calculus'. For more lecture videos and $10 digital textbooks, visit www.centerofmath.org.
From playlist Multivariable Integrals
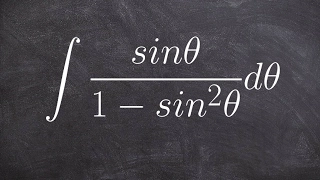
Find the antiderivative using pythagorean trigonometric identities
👉 Learn how to evaluate the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which t
From playlist The Integral