
Linear Algebra: Continuing with function properties of linear transformations, we recall the definition of an onto function and give a rule for onto linear transformations.
From playlist MathDoctorBob: Linear Algebra I: From Linear Equations to Eigenspaces | CosmoLearning.org Mathematics

Stable Homotopy Seminar, 18: The Steenrod Algebra (Liam Keenan)
Liam defines the Steenrod algebra, as the endomorphisms of the Eilenberg-MacLane spectrum HF_p. This naturally acts on the mod p cohomology of any space (or spectrum), and we look at the example of the mod 2 cohomology of RP^infinity. He states some of its fundamental properties allowing u
From playlist Stable Homotopy Seminar

10A An Introduction to Eigenvalues and Eigenvectors
A short description of eigenvalues and eigenvectors.
From playlist Linear Algebra

CU Boulder 2020 Mathematics Virtual Graduation Ceremony
Congratulations to the Mathematics Class of 2020
From playlist My Students

Linear algebra for Quantum Mechanics
Linear algebra is the branch of mathematics concerning linear equations such as. linear functions and their representations in vector spaces and through matrices. In this video you will learn about #linear #algebra that is used frequently in quantum #mechanics or #quantum #physics. ****
From playlist Quantum Physics

Homological Algebra(Homo Alg) 4 by Graham Ellis
DATE & TIME 05 November 2016 to 14 November 2016 VENUE Ramanujan Lecture Hall, ICTS Bangalore Computational techniques are of great help in dealing with substantial, otherwise intractable examples, possibly leading to further structural insights and the detection of patterns in many abstra
From playlist Group Theory and Computational Methods

Stable Homotopy Seminar, 21: Computing Homotopy Groups with the Adams Spectral Sequence (Zach Himes)
Zachary Himes constructs the May spectral sequence, a tool using a filtration of of the dual Steenrod algebra that calculates the E2 page of the Adams spectral sequence. May's original insight was that the associated graded of the dual Steenrod algebra is a primitively generated Hopf algeb
From playlist Stable Homotopy Seminar

Linear Algebra 7.4 Optimization Using Quadratic Forms
My notes are available at http://asherbroberts.com/ (so you can write along with me). Elementary Linear Algebra: Applications Version 12th Edition by Howard Anton, Chris Rorres, and Anton Kaul A. Roberts is supported in part by the grants NSF CAREER 1653602 and NSF DMS 2153803.
From playlist Linear Algebra

Stable Homotopy Seminar, 20: Computations with the Adams Spectral Sequence (Jacob Hegna)
Jacob Hegna walks us through some of the methods which have been used to compute the E_2 page of the Adams spectral sequence for the sphere, a.k.a. Ext_A(F_2, F_2), where A is the Steenrod algebra. The May spectral sequence works by filtering A and first computing Ext over the associated g
From playlist Stable Homotopy Seminar
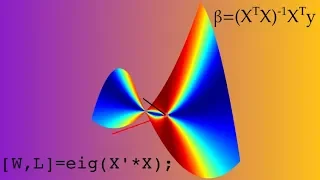
This is part of an online course on beginner/intermediate linear algebra, which presents theory and implementation in MATLAB and Python. The course is designed for people interested in applying linear algebra to applications in multivariate signal processing, statistics, and data science.
From playlist Linear algebra: theory and implementation

Algebra - Ch. 4: Exponents & Scientific Notation (1 of 35) What is an Exponent?
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain what is an exponent. A number or symbol placed above another number or symbol that indicates the power the number or symbol at the bottom is raised. The number at the bottom is called the base
From playlist ALGEBRA CH 4 EXPONENTS AND SCIENTIFIC NOTATION

Sergey Melikhov, Steklov Math Institute (Moscow) Title: Fine Shape Abstract: A shape theory is something which is supposed to agree with homotopy theory on polyhedra and to treat more general spaces by looking at their polyhedral approximations. Or if you prefer, it is something which is s
From playlist 39th Annual Geometric Topology Workshop (Online), June 6-8, 2022

Jeremy Dubut: Natural homology computability and Eilenberg Steenrod axioms
The lecture was held within the framework of the Hausdorff Trimester Program : Applied and Computational Algebraic Topology
From playlist HIM Lectures: Special Program "Applied and Computational Algebraic Topology"

Lecture 8: Bökstedt Periodicity
In this video, we give a proof of Bökstedts fundamental result showing that THH of F_p is polynomial in a degree 2 class. This will rely on unlocking its relation to the dual Steenrod algebra and the fundamental fact, that the latter is free as an E_2-Algebra. Feel free to post comments a
From playlist Topological Cyclic Homology

Abstract Algebra: The definition of a Ring
Learn the definition of a ring, one of the central objects in abstract algebra. We give several examples to illustrate this concept including matrices and polynomials. Be sure to subscribe so you don't miss new lessons from Socratica: http://bit.ly/1ixuu9W ♦♦♦♦♦♦♦♦♦♦ We recommend th
From playlist Abstract Algebra

Anibal Medina, "Persistence Steenrod modules"
The talk is part of the Workshop Topology of Data in Rome (15-16/09/2022) https://www.mat.uniroma2.it/Eventi/2022/Topoldata/topoldata.php The event was organized in partnership with the Romads Center for Data Science https://www.mat.uniroma2.it/~rds/about.php The Workshop was hosted and
From playlist Workshop: Topology of Data in Rome

Algebra for Beginners | Basics of Algebra
#Algebra is one of the broad parts of mathematics, together with number theory, geometry and analysis. In its most general form, algebra is the study of mathematical symbols and the rules for manipulating these symbols; it is a unifying thread of almost all of mathematics. Table of Conten
From playlist Linear Algebra

Units in a Ring (Abstract Algebra)
The units in a ring are those elements which have an inverse under multiplication. They form a group, and this “group of units” is very important in algebraic number theory. Using units you can also define the idea of an “associate” which lets you generalize the fundamental theorem of ar
From playlist Abstract Algebra

Introduction to Fiber Bundles part 1: Definitions
We give the definition of a fiber bundle with fiber F, trivializations and transition maps. This is a really basic stuff that we use a lot. Here are the topics this sets up: *Associated Bundles/Principal Bundles *Reductions of Structure Groups *Steenrod's Theorem *Torsor structure on arith
From playlist Fiber bundles
