
http://www.teachastronomy.com/ Cosmology is the study of the universe, its history, and everything in it. It comes from the Greek root of the word cosmos for order and harmony which reflected the Greek belief that the universe was a harmonious entity where everything worked in concert to
From playlist 22. The Big Bang, Inflation, and General Cosmology

Trigonometry 5 The Cosine Relationship
A geometrical explanation of the law of cosines.
From playlist Trigonometry

From playlist Courses and Series

Trigonometry 7 The Cosine of the Sum and Difference of Two Angles
A geometric proof of the cosine of the sum and difference of two angles identity.
From playlist Trigonometry

Using the law of cosines for a triangle with SAS
Learn how to solve for the lengths of the sides and the measures of the angles of a triangle using the law of cosines. The law of cosines is used in determining the lengths of the sides or the measures of the angles of a triangle when no angle measure and the length of the side opposite th
From playlist Law of Cosines
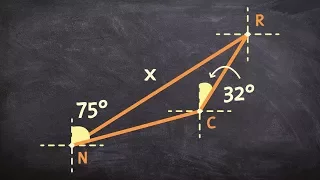
Applying the law of cosines to solve a word problem
Learn how to solve for the lengths of the sides and the measures of the angles of a triangle using the law of cosines. The law of cosines is used in determining the lengths of the sides or the measures of the angles of a triangle when no angle measure and the length of the side opposite th
From playlist Solve Law of Cosines (Word Problem) #ObliqueTriangles

How to use law of cosines for SSS
Learn how to solve for the lengths of the sides and the measures of the angles of a triangle using the law of cosines. The law of cosines is used in determining the lengths of the sides or the measures of the angles of a triangle when no angle measure and the length of the side opposite th
From playlist Law of Cosines

A Riemann-Roch theorem in Bott-Chern cohomology - Jean-Michel Bismut
Jean-Michel Bismut Université Paris-Sud April 21, 2014 If MM is a complex manifold, the Bott-Chern cohomology H(⋅,⋅)BC(M,C)HBC(⋅,⋅)(M,C) of MM is a refinement of de Rham cohomology, that takes into account the p,q p,q grading of smooth differential forms. By results of Bott and Chern, vect
From playlist Mathematics

Coulomb's Law (3 of 7) Force Between Two One Coulomb Charges
Using Coulomb's law shows how to calculate the electric force between two 1 Coulombs charges that are separated by a distance of 1 meter. Coulomb's law states that the magnitude of the force between two point charges is directly proportional to the product of the magnitudes of charges and
From playlist Coulomb's Law and the Electric Force

Cong Xue - 2/2 Cohomology Sheaves of Stacks of Shtukas
Cohomology sheaves and cohomology groups of stacks of shtukas are used in the Langlands program for function fields. We will explain (1) how the Eichler-Shimura relations imply the finiteness property of the cohomology groups, (2) how the finiteness and Drinfeld's lemma imply the action of
From playlist 2022 Summer School on the Langlands program
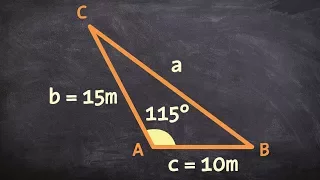
Applying the law of cosines when given SAS
Learn how to solve for the lengths of the sides and the measures of the angles of a triangle using the law of cosines. The law of cosines is used in determining the lengths of the sides or the measures of the angles of a triangle when no angle measure and the length of the side opposite th
From playlist Law of Cosines

Stable Homotopy without Homotopy - Toni Mikael Annala
IAS/Princeton Arithmetic Geometry Seminar Topic: Stable Homotopy without Homotopy Speaker: Toni Mikael Annala Affiliation: Member, School of Mathematics Date: January 30, 2023 Many cohomology theories in algebraic geometry, such as crystalline and syntomic cohomology, are not homotopy in
From playlist Mathematics

Duality for Rabinowitz-Floer homology - Alex Oancea
IAS/PU-Montreal-Paris-Tel-Aviv Symplectic Geometry Topic: Duality for Rabinowitz-Floer homology Speaker: Alex Oancea Affiliation: Institut de Mathématiques de Jussieu-Paris Rive Gauche Date: May 27, 2020 For more video please visit http://video.ias.edu
From playlist PU/IAS Symplectic Geometry Seminar

Categorical aspects of vortices (Lecture 2) by Niklas Garner
PROGRAM: VORTEX MODULI ORGANIZERS: Nuno Romão (University of Augsburg, Germany) and Sushmita Venugopalan (IMSc, India) DATE & TIME: 06 February 2023 to 17 February 2023 VENUE: Ramanujan Lecture Hall, ICTS Bengaluru For a long time, the vortex equations and their associated self-dual fie
From playlist Vortex Moduli - 2023

Cong Xue - 1/2 Cohomology Sheaves of Stacks of Shtukas
Cohomology sheaves and cohomology groups of stacks of shtukas are used in the Langlands program for function fields. We will explain (1) how the Eichler-Shimura relations imply the finiteness property of the cohomology groups, (2) how the finiteness and Drinfeld's lemma imply the action of
From playlist 2022 Summer School on the Langlands program

Tim Perutz: From categories to curve-counts in mirror symmetry
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Jean-Morlet Chair - Lalonde/Teleman

The cup product operation [Ling Zhou]
In this tutorial, you will learn about the cup product operation in the simplicial setting, and go through an example of computing it in the 2-torus. The cup product induces a ring structure on cohomology, making it more informative than homology. In the TDA community, many attentions have
From playlist Tutorial-a-thon 2021 Fall

Categorical aspects of vortices (Lecture 1) by Niklas Garner
PROGRAM: VORTEX MODULI ORGANIZERS: Nuno Romão (University of Augsburg, Germany) and Sushmita Venugopalan (IMSc, India) DATE & TIME: 06 February 2023 to 17 February 2023 VENUE: Ramanujan Lecture Hall, ICTS Bengaluru For a long time, the vortex equations and their associated self-dual fie
From playlist Vortex Moduli - 2023

Sylvia Serfaty: Microscopic description of Coulomb gases
We are interested in the statistical mechanics of systems of N points with Coulomb interactions in general dimension for a broad temperature range. We discuss local laws characterizing the rigidity of the system at the microscopic level, as well as free energy expansion and Central Limit T
From playlist Analysis and its Applications

Lars Hesselholt: Around topological Hochschild homology (Lecture 8)
The lecture was held within the framework of the (Junior) Hausdorff Trimester Program Topology: "Workshop: Hermitian K-theory and trace methods" Introduced by Bökstedt in the late eighties, topological Hochschild homology is a manifestation of the dual visions of Connes and Waldhausen to
From playlist HIM Lectures: Junior Trimester Program "Topology"