
Topology (What is a Topology?)
What is a Topology? Here is an introduction to one of the main areas in mathematics - Topology. #topology Some of the links below are affiliate links. As an Amazon Associate I earn from qualifying purchases. If you purchase through these links, it won't cost you any additional cash, b
From playlist Topology

I define closed sets, an important notion in topology and analysis. It is defined in terms of limit points, and has a priori nothing to do with open sets. Yet I show the important result that a set is closed if and only if its complement is open. More topology videos can be found on my pla
From playlist Topology

What Is Network Topology? | Types of Network Topology | BUS, RING, STAR, TREE, MESH | Simplilearn
In this video on Network Topology, we will understand What is Network topology, the role of using topology while designing a network, Different types of Topologies in a Network. Network topology provides us with a way to configure the most optimum network design according to our requiremen
From playlist Cyber Security Playlist [2023 Updated]🔥

In this video, I cover the notion of continuity, as used in topology. The beautiful thing is that this doesn't use epsilon-delta at all, and instead just something purely geometric. Enjoy this topology-adventure! Topology Playlist: https://youtube.com/playlist?list=PLJb1qAQIrmmA13vj9xkHGG
From playlist Topology

Topology 1.3 : Basis for a Topology
In this video, I define what a basis for a topology is. Email : fematikaqna@gmail.com Code : https://github.com/Fematika/Animations Notes : None yet
From playlist Topology

Topology 1.1 : Open Sets of Reals
In this video, I give a definition of the open sets on the real numbers. Email : fematikaqna@gmail.com Code : https://github.com/Fematika/Animations Notes : None yet
From playlist Topology

In this video, I define connectedness, which is a very important concept in topology and math in general. Essentially, it means that your space only consists of one piece, whereas disconnected spaces have two or more pieces. I also define the related notion of path-connectedness. Topology
From playlist Topology

Teach Astronomy - Topology of the Universe
http://www.teachastronomy.com/ Astronomers sometimes talk about the topology of the universe which is a mathematical description of the three dimensional structure in terms of mathematical shapes. Using this formalism astronomers are of course simplifying something that's actually very co
From playlist 20. Galaxy Interaction and Motion
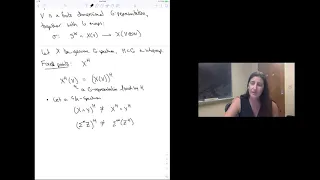
Teena Gerhardt - 2/3 Algebraic K-theory and Trace Methods
Algebraic K-theory is an invariant of rings and ring spectra which illustrates a fascinating interplay between algebra and topology. Defined using topological tools, this invariant has important applications to algebraic geometry, number theory, and geometric topology. One fruitful approac
From playlist Summer School 2020: Motivic, Equivariant and Non-commutative Homotopy Theory

Teena Gerhardt - 3/3 Algebraic K-theory and Trace Methods
Algebraic K-theory is an invariant of rings and ring spectra which illustrates a fascinating interplay between algebra and topology. Defined using topological tools, this invariant has important applications to algebraic geometry, number theory, and geometric topology. One fruitful approac
From playlist Summer School 2020: Motivic, Equivariant and Non-commutative Homotopy Theory

Commutative algebra 13 (Topology of Spec R)
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. In this lecture we discuss the topology of the spectrum Spec R of a ring, showing that it is compact, sometimes connected, an
From playlist Commutative algebra

Topology 1.7 : More Examples of Topologies
In this video, I introduce important examples of topologies I didn't get the chance to get to. This includes The discrete and trivial topologies, subspace topology, the lower-bound and K topologies on the reals, the dictionary order, and the line with two origins. I also introduce (again)
From playlist Topology

Geometric Representation of Structured Extensions in Ergodic Theory - Henrik Kreidler
Special Year Research Seminar Topic: Geometric Representation of Structured Extensions in Ergodic Theory Speaker: Henrik Kreidler Affiliation: Bergische Universität Wuppertal Date: March 14, 2023 The Mackey-Zimmer representation theorem is a key structural result from ergodic theory: Eve
From playlist Mathematics

MagLab Theory Winter School 2018: Duncan Haldane - Bipartite Entanglement I
The National MagLab held it's sixth Theory Winter School in Tallahassee, FL from January 8th - 13th, 2018.
From playlist 2018 Theory Winter School

Commutative algebra 11 (Spectrum of a ring)
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. In this lecture we define the spectrum of a ring as the space of prime ideals, and give a few examples. Reading: Lectures 9
From playlist Commutative algebra

Schemes 5: Definition of a scheme
This lecture is part of an online algebraic geometry course on schemes, based on chapter II of "Algebraic geometry" by Hartshorne. We give some historical background, then give the definition of a scheme and some simple examples, and finish by explaining the origin of the word "spectrum".
From playlist Algebraic geometry II: Schemes

Supersymmetry on the lattice: Geometry, Topology, and Spin Liquids by Simon Trebst
PROGRAM FRUSTRATED METALS AND INSULATORS (HYBRID) ORGANIZERS Federico Becca (University of Trieste, Italy), Subhro Bhattacharjee (ICTS-TIFR, India), Yasir Iqbal (IIT Madras, India), Bella Lake (Helmholtz-Zentrum Berlin für Materialien und Energie, Germany), Yogesh Singh (IISER Mohali, In
From playlist FRUSTRATED METALS AND INSULATORS (HYBRID, 2022)

Hermann Schulz-Baldes: Computational K-theory via the spectral localizer.
Talk by Hermann Schulz-Baldes in Global Noncommutative Geometry Seminar (Europe) http://www.noncommutativegeometry.nl/ncgseminar/ on March 24, 2021
From playlist Global Noncommutative Geometry Seminar (Europe)

Rings 6 Prime and maximal ideals
This lecture is part of an online course on rings and modules. We discuss prime and maximal ideals of a (commutative) ring, use them to construct the spectrum of a ring, and give a few examples. For the other lectures in the course see https://www.youtube.com/playlist?list=PL8yHsr3EFj5
From playlist Rings and modules

Definition of a Topological Space
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Definition of a Topological Space
From playlist Topology