
Xiaolu Tan: On the martingale optimal transport duality in the Skorokhod space
We study a martingale optimal transport problem in the Skorokhod space of cadlag paths, under finitely or infinitely many marginals constraint. To establish a general duality result, we utilize a Wasserstein type topology on the space of measures on the real value space, and the S-topology
From playlist HIM Lectures 2015

Adam Jakubowski: Functional convergence for dependent heavy-tailed models
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Probability and Statistics

Gaoyue Guo - Optimal Skorokhod embedding problem
http://www.lesprobabilitesdedemain.fr/index.html Organisateurs : Céline Abraham, Linxiao Chen, Pascal Maillard, Bastien Mallein et la Fondation Sciences Mathématiques de Paris
From playlist Les probabilités de demain 2016

Maxim Konsevitch - 1/4 Exponential Integral
Summary : https://indico.math.cnrs.fr/getFile.py/access?resId=0&materialId=3&confId=694 The goal of the first part of the course is to describe and compare various cohomology theories for algebraic varieties endowed with global function. In the second part infinite-dimensional application
From playlist Maxim Konsevitch - Exponential Integral

Maxim Konsevitch - 2/4 Exponential Integral
Summary : https://indico.math.cnrs.fr/getFile.py/access?resId=0&materialId=3&confId=694 The goal of the first part of the course is to describe and compare various cohomology theories for algebraic varieties endowed with global function. In the second part infinite-dimensional application
From playlist Maxim Konsevitch - Exponential Integral

Optimal Transportation and Applications - 12 November 2018
http://crm.sns.it/event/436 It is the ninth edition of this "traditional'' meeting in Pisa, after the ones in 2001, 2003, 2006, 2008, 2010, 2012, 2014 and 2016. Organizing Committee Luigi Ambrosio, Scuola Normale Superiore, Pisa Giuseppe Buttazzo, Dipartimento di Matematica, Università
From playlist Centro di Ricerca Matematica Ennio De Giorgi

Maxim Konsevitch - 3/4 Exponential Integral
Summary : https://indico.math.cnrs.fr/getFile.py/access?resId=0&materialId=3&confId=694 The goal of the first part of the course is to describe and compare various cohomology theories for algebraic varieties endowed with global function. In the second part infinite-dimensional application
From playlist Maxim Konsevitch - Exponential Integral

What is an integral and it's parts
👉 Learn about integration. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which the upper and the lower li
From playlist The Integral

Integrate cosine using u substitution
👉 Learn how to evaluate the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which t
From playlist The Integral

In this video, the last one of the integral-trilogy, I find the antiderivative of the square root of x^2 - 1. The method is surprisingly similar to the one of the square root of x^2 + 1, and I recommend you see that one first, because it uses the formula for the integral of sec^3, which I
From playlist Integrals

Use the FTOC to evaluate the integral
Keywords 👉 Learn how to evaluate the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as indefinite integral or as a definite integral. A definite integral is an integral in
From playlist Evaluate Integrals

Quantum Integral. Gauss would be proud! I calculate the integral of x^2n e^-x^2 from -infinity to infinity, using Feynman's technique, as well as the Gaussian integral and differentiation. This integral appears over and over again in quantum mechanics and is useful for calculus and physics
From playlist Integrals
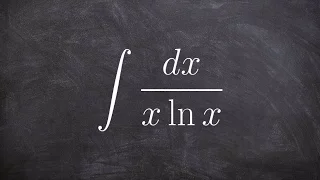
How to u substitution to natural logarithms
👉 Learn how to evaluate the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which t
From playlist The Integral

MATH2018 Lecture 4.1 Double Integrals
Double integration extends the concepts of regular integration to functions of more than one variable. Instead of finding the area under a curve, we will be calculating the volume under a surface.
From playlist MATH2018 Engineering Mathematics 2D

Lecture 12: Lebesgue Integrable Functions, the Lebesgue Integral and the Dominated Convergence...
MIT 18.102 Introduction to Functional Analysis, Spring 2021 Instructor: Dr. Casey Rodriguez View the complete course: https://ocw.mit.edu/courses/18-102-introduction-to-functional-analysis-spring-2021/ YouTube Playlist: https://www.youtube.com/watch?v=W2pw1JWc9k4&list=PLUl4u3cNGP63micsJp_
From playlist MIT 18.102 Introduction to Functional Analysis, Spring 2021

All calculus integration techniques: Integration by parts, DI method, reverse power rule, u-substitution, trigonometric substitution, integration by substitution, integration by partial fraction decomposition, trigonometric integrals, and more. An extreme calculus tutorial by @blackpenredp
From playlist 100 Everything
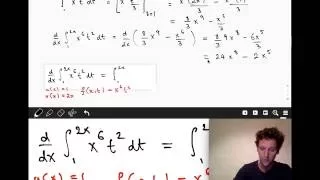
MATH2018 Lecture 1.4 Liebniz' Rule
Liebniz' Rule tells us how to deal with the case when we differentiate an integral of a function of more than one variable.
From playlist MATH2018 Engineering Mathematics 2D

Worldwide Calculus: Improper Integrals
Lecture on 'Improper Integrals' from 'Worldwide Integral Calculus' and 'Worldwide AP Calculus'. For more lecture videos and $10 digital textbooks, visit www.centerofmath.org.
From playlist Continuous Sums: the Definite Integral

Worldwide Calculus: Integration in R²
Lecture on 'Integration in R²' from 'Worldwide Multivariable Calculus'. For more lecture videos and $10 digital textbooks, visit www.centerofmath.org.
From playlist Multivariable Integrals

What is the constant rule of integration
👉 Learn how to evaluate the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which t
From playlist The Integral