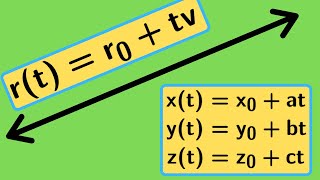Mathematical concepts | Surfaces | Geometry
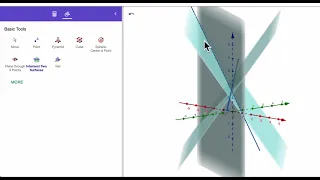
Sheaf of planes
In mathematics, a sheaf of planes is the set of all planes that have the same common line. It may also be known as a fan of planes or a pencil of planes. When extending the concept of line to the line at infinity, a set of parallel planes can be seen as a sheaf of planes intersecting in a line at infinity. To distinguish it from the more general definition, the adjective parallel can be added to it, resulting in the expression parallel sheaf of planes. (Wikipedia).