
The Schwarz Lemma -- Complex Analysis
Part 1 -- The Maximum Principle: https://youtu.be/T_Msrljdtm4 Part 3 -- Liouville's theorem: https://www.youtube.com/watch?v=fLnRDhhzWKQ In today's video, we want to take a look at the Schwarz lemma — this is a monumental result in the subject of one complex variable, and has lead to many
From playlist Complex Analysis

Complex Analysis (Advanced) -- The Schwarz Lemma
A talk I gave concerning my recent results on the Schwarz Lemma in Kähler and non-Kähler geometry. The talk details the classical Schwarz Lemma and discusses André Bloch. This is part 1 of a multi-part series. Part 1 -- https://youtu.be/AWqeIPMNhoA Part 2 -- https://youtu.be/hd7-iio77kc P
From playlist Complex Analysis

Complex Analysis (Advanced) -- The Schwarz--Pick Lemma -- The First Divide
Excerpt from a talk I gave concerning my recent results on the Schwarz Lemma in Kähler and non-Kähler geometry. The talk details the classical Schwarz Lemma and discusses André Bloch. This is part 5 of a multi-part series. Part 1 -- https://youtu.be/AWqeIPMNhoA Part 2 -- https://youtu.be/
From playlist Complex Analysis

Kyle Broder -- Recent Developments Concerning the Schwarz Lemma
A lecture I gave at the Beijing International Center for Mathematical Research geometric analysis seminar. The title being Recent Developments Concerning the Schwarz Lemma with applications to the Wu--Yau Theorem. This contains some recent results concerning the Bochner technique for the G
From playlist Research Lectures
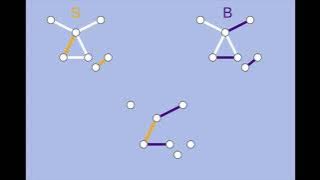
Berge's lemma, an animated proof
Berge's lemma is a mathematical theorem in graph theory which states that a matching in a graph is of maximum cardinality if and only if it has no augmenting paths. But what do those terms even mean? And how do we prove Berge's lemma to be true? == CORRECTION: at 7:50, the red text should
From playlist Summer of Math Exposition Youtube Videos

Complex Analysis (Advanced) -- This murderer inspired the results of my Ph.D. thesis
Excerpt from a talk I gave concerning my recent results on the Schwarz Lemma in Kähler and non-Kähler geometry. The talk details the classical Schwarz Lemma and discusses André Bloch. This is part 1 of a multi-part series. Part 1 -- https://youtu.be/AWqeIPMNhoA Part 2 -- https://youtu.be/
From playlist Complex Analysis
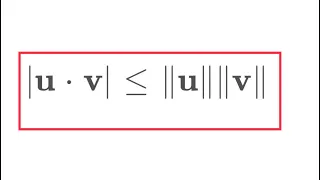
This is one of my favorite math proofs! Usually the Cauchy-Schwarz inequality is proven using projections, but this proof is completely elementary. It is taken from Pugh's Real Mathematical Analysis-book. But beware it doesn't work for complex inner product spaces. Bon appétit! :) Note: I
From playlist Orthogonality

Burnside's Lemma (Part 2) - combining math, science and music
Part 1 (previous video): https://youtu.be/6kfbotHL0fs Orbit-stabilizer theorem: https://youtu.be/BfgMdi0OkPU Burnside's lemma is an interesting result in group theory that helps us count things with symmetries considered, e.g. in some situations, we don't want to count things that can be
From playlist Traditional topics, explained in a new way

Liouville's theorem -- Complex Analysis
In this video, we give a proof of Liouville's theorem: A bounded entire function is constant. This uses the Schwarz Lemma that was proved in a previous video: https://www.youtube.com/watch?v=jmP4VlgZvb0 Other videos in this series on complex analysis include: The Schwarz Lemma: https://ww
From playlist Complex Analysis

11. Pseudorandom graphs I: quasirandomness
MIT 18.217 Graph Theory and Additive Combinatorics, Fall 2019 Instructor: Yufei Zhao View the complete course: https://ocw.mit.edu/18-217F19 YouTube Playlist: https://www.youtube.com/playlist?list=PLUl4u3cNGP62qauV_CpT1zKaGG_Vj5igX Prof. Zhao discusses a classic result of Chung, Graham, a
From playlist MIT 18.217 Graph Theory and Additive Combinatorics, Fall 2019

Alexandre Sukhov - J-complex curves: some applications (Part 3)
We will focus in our lectures on the following : 1. J-complex discs in almost complex manifolds : general properties. Linearization and compactness. Gromov’s method : the Fredholm alternative for the d-bar operator. Attaching a complex disc to a Lagrangian manifold. Application : exotic sy
From playlist École d’été 2012 - Feuilletages, Courbes pseudoholomorphes, Applications

The Green-Tao theorem and a relative Szemeredi theorem - Yufei Zhao
Slides for this talk: https://drive.google.com/file/d/1RdgY6N869MN5lJwl2jv1HwIgWky6aW5C/view?usp=sharing The Green-Tao theorem and a relative Szemeredi theorem - Yufei Zhao Abstract: The celebrated Green-Tao theorem states that there are arbitrarily long arithmetic progressions in the p
From playlist Mathematics

Graph regularity and counting lemmas - Jacob Fox
Conference on Graphs and Analysis Jacob Fox June 5, 2012 More videos on http://video.ias.edu
From playlist Mathematics

In this video, I prove the famous Riemann-Lebesgue lemma, which states that the Fourier transform of an integrable function must go to 0 as |z| goes to infinity. This is one of the results where the proof is more important than the theorem, because it's a very classical Lebesgue integral
From playlist Real Analysis