
Understanding and computing the Riemann zeta function
In this video I explain Riemann's zeta function and the Riemann hypothesis. I also implement and algorithm to compute the return values - here's the Python script:https://gist.github.com/Nikolaj-K/996dba1ff1045d767b10d4d07b1b032f
From playlist Programming

An invitation to higher Teichmüller theory – Anna Wienhard – ICM2018
Geometry Invited Lecture 5.11 An invitation to higher Teichmüller theory Anna Wienhard Abstract: Riemann surfaces are of fundamental importance in many areas of mathematics and theoretical physics. The study of the moduli space of Riemann surfaces of a fixed topological type is intimatel
From playlist Geometry
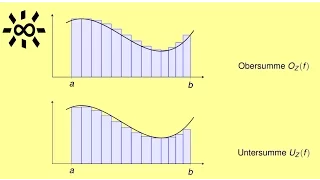
Abonniert den Kanal oder unterstützt ihn auf Steady: https://steadyhq.com/en/brightsideofmaths Ihr werdet direkt informiert, wenn ich einen Livestream anbiete. Hier erkläre ich kurz das Riemann-Integral mit Ober- und Untersumme. Die Definition ist übliche, die im 1. Semester eingeführt w
From playlist Analysis

Some identities involving the Riemann-Zeta function.
After introducing the Riemann-Zeta function we derive a generating function for its values at positive even integers. This generating function is used to prove two sum identities. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist The Riemann Zeta Function

What is the Riemann Hypothesis?
This video provides a basic introduction to the Riemann Hypothesis based on the the superb book 'Prime Obsession' by John Derbyshire. Along the way I look at convergent and divergent series, Euler's famous solution to the Basel problem, and the Riemann-Zeta function. Analytic continuation
From playlist Mathematics

Riemann Sum Defined w/ 2 Limit of Sums Examples Calculus 1
I show how the Definition of Area of a Plane is a special case of the Riemann Sum. When finding the area of a plane bound by a function and an axis on a closed interval, the width of the partitions (probably rectangles) does not have to be equal. I work through two examples that are rela
From playlist Calculus
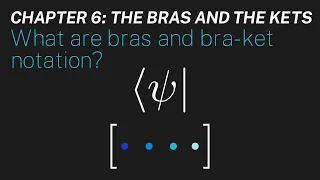
Ch 6: What are bras and bra-ket notation? | Maths of Quantum Mechanics
Hello! This is the sixth chapter in my series "Maths of Quantum Mechanics." In this episode, we'll intuitively understand what the bra is in quantum mechanics, and why we need it. We'll also finally justify the power of bra-ket notation, and its relation to the Riesz representation theore
From playlist Maths of Quantum Mechanics

Functional Analysis - Part 15 - Riesz Representation Theorem
Support the channel on Steady: https://steadyhq.com/en/brightsideofmaths Or support me via PayPal: https://paypal.me/brightmaths Functional analysis series: https://www.youtube.com/playlist?list=PLBh2i93oe2qsGKDOsuVVw-OCAfprrnGfr PDF versions: https://steadyhq.com/en/brightsideofmaths/po
From playlist Functional analysis

Functional Analysis Lecture 07 2014 02 11 Riesz Interpolation Theorem, Part 2
Proof of theorem in case of general L^p functions. Using Riesz interpolation to extend Fourier transform. Rapidly decreasing functions; Schwartz class functions. Fourier transform of a Schwartz class function. Properties of Fourier transform (interaction with basic operations); Fourie
From playlist Course 9: Basic Functional and Harmonic Analysis

Sir Michael Atiyah | The Riemann Hypothesis | 2018
Slides for this talk: https://drive.google.com/file/d/1DNHG9TDXiVslO-oqDud9f-9JzaFCrHxl/view?usp=sharing Sir Michael Francis Atiyah: "The Riemann Hypothesis" Monday September 24, 2018 9:45 Abstract: The Riemann Hypothesis is a famous unsolved problem dating from 1859. I will present a
From playlist Number Theory

A (compelling?) reason for the Riemann Hypothesis to be true #SOME2
A visual walkthrough of the Riemann Zeta function and a claim of a good reason for the truth of the Riemann Hypothesis. This is not a formal proof but I believe the line of argument could lead to a formal proof.
From playlist Summer of Math Exposition 2 videos

Gravitational radiation from post-Newtonian sources.... by Luc Blanchet (Lecture - 3)
PROGRAM SUMMER SCHOOL ON GRAVITATIONAL WAVE ASTRONOMY ORGANIZERS : Parameswaran Ajith, K. G. Arun and Bala R. Iyer DATE : 15 July 2019 to 26 July 2019 VENUE : Madhava Lecture Hall, ICTS Bangalore This school is part of the annual ICTS summer schools on gravitational-wave (GW) astronomy.
From playlist Summer School on Gravitational Wave Astronomy -2019

MATH331: Riemann Surfaces - part 1
We define what a Riemann Surface is. We show that PP^1 is a Riemann surface an then interpret our crazy looking conditions from a previous video about "holomorphicity at infinity" as coming from the definition of a Riemann Surface.
From playlist The Riemann Sphere

Math 131 Spring 2022 050422 Riesz Fischer; Parseval's theorem
Riesz-Fischer theorem: Fourier Series of a (Riemann integrable) function converge to the original function - in the L2 sense. Consequence: Parseval's theorem: the L2 norm of the function is the l2 norm of its Fourier coefficients.
From playlist Math 131 Spring 2022 Principles of Mathematical Analysis (Rudin)

Background material on the Cauchy-Riemann equations (Lecture 1) by Debraj Chakrabarti
PROGRAM CAUCHY-RIEMANN EQUATIONS IN HIGHER DIMENSIONS ORGANIZERS: Sivaguru, Diganta Borah and Debraj Chakrabarti DATE: 15 July 2019 to 02 August 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Complex analysis is one of the central areas of modern mathematics, and deals with holomo
From playlist Cauchy-Riemann Equations in Higher Dimensions 2019

Pablo Ochoa: Capacity based cond for existence of sol. to f / e problems with 1st-order terms
In this talk, we will discuss the existence of distributional solutions to fractional elliptic problems with non-linear first-order terms and measure data ! in RN. It is well-known in the literature that solutions to elliptic problems with superlinear growth in the gradient exist if the so
From playlist Hausdorff School: Trending Tools

Michael Baake: A cocycle approach to the Fourier transform of Rauzy fractals...
"A cocycle approach to the Fourier transform of Rauzy fractals and the point spectrumof Pisot inflation tilings" The lecture was held within the framework of the Hausdorff Trimester Program "Dynamics: Topology and Numbers": Conference on “Transfer operators in number theory and quantum ch
From playlist Conference: Transfer operators in number theory and quantum chaos

Endre Szemerédi - The Abel Prize interview 2012
0:28 Early interest in mathematics 3:01 High schools in Hungary specializing in mathematics 4:38 Started studying mathematics at the age of 22 7:24 Professor Paul Turán inspired me to become a mathematician 8:57 Relationship between Paul Turán and Atle Selberg 9:24 Other influences and col
From playlist Endre Szemerédi

Definition of Area Riemann Sum Limit of Sums Part 2 of 2 Calculus 1
I introduce the Definition of Area of a Plane. This is a special case of Riemann Sums where the width of the rectangles used to find the area of a plane bound by a function and the x-axis are all of equal width. Many examples are worked through. This is part 2 of my video "Area of a Pl
From playlist Calculus
