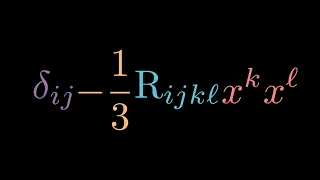
Curvature of a Riemannian Manifold | Riemannian Geometry
In this lecture, we define the exponential mapping, the Riemannian curvature tensor, Ricci curvature tensor, and scalar curvature. The focus is on an intuitive explanation of the curvature tensors. The curvature tensor of a Riemannian metric is a very large stumbling block for many student
From playlist All Videos

Riemann Sum Defined w/ 2 Limit of Sums Examples Calculus 1
I show how the Definition of Area of a Plane is a special case of the Riemann Sum. When finding the area of a plane bound by a function and an axis on a closed interval, the width of the partitions (probably rectangles) does not have to be equal. I work through two examples that are rela
From playlist Calculus

D. Tewodrose - Limits of Riemannian manifolds satisfying a uniform Kato condition
I will present a joint work with G. Carron and I. Mondello where we study Kato limit spaces. These are metric measure spaces obtained as Gromov-Hausdorff limits of smooth n-dimensional Riemannian manifolds with Ricci curvature satisfying a uniform Kato-type condition. In this context, stri
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

Convergence and Riemannian bounds on Lagrangian submanifolds - Jean-Philippe Chassé
Joint IAS/Princeton/Montreal/Paris/Tel-Aviv Symplectic Geometry Title: Convergence and Riemannian bounds on Lagrangian submanifolds Speaker: Jean-Philippe Chassé Affiliation: UdeM Date: October 8, 2021 Abstract: Recent years have seen the appearance of a plethora of possible metrics on
From playlist PU/IAS Symplectic Geometry Seminar

Measures on spaces of Riemannian metrics - Dmitry Jakobson
Dmitry Jakobson McGill University July 21, 2014 This is joint work with Y. Canzani, B. Clarke, N. Kamran, L. Silberman and J. Taylor. We construct Gaussian measure on the manifold of Riemannian metrics with the fixed volume form. We show that diameter and Laplace eigenvalue and volume entr
From playlist Mathematics

Lecture 15: Isometries, Rigidity, and Curvature
CS 468: Differential Geometry for Computer Science
From playlist Stanford: Differential Geometry for Computer Science (CosmoLearning Computer Science)

Z. Badreddine - Optimal transportation problem and MCP property on sub-Riemannian structures
This presentation is devoted to the study of mass transportation on sub-Riemannian geometry. In order to obtain existence and uniqueness of optimal transport maps, the first relevant method to consider is the one used by Figalli and Rifford which is based on the local semiconcavity of the
From playlist Journées Sous-Riemanniennes 2018

How to find the position function given the acceleration function
👉 Learn how to approximate the integral of a function using the Reimann sum approximation. Reimann sum is an approximation of the area under a curve or between two curves by dividing it into multiple simple shapes like rectangles and trapezoids. In using the Reimann sum to approximate the
From playlist Riemann Sum Approximation

Symmetric spaces (Lecture - 3) by Pralay Chatterjee
Geometry, Groups and Dynamics (GGD) - 2017 DATE: 06 November 2017 to 24 November 2017 VENUE: Ramanujan Lecture Hall, ICTS, Bengaluru The program focuses on geometry, dynamical systems and group actions. Topics are chosen to cover the modern aspects of these areas in which research has b
From playlist Geometry, Groups and Dynamics (GGD) - 2017

Riemannian Geometry - Definition: Oxford Mathematics 4th Year Student Lecture
Riemannian Geometry is the study of curved spaces. It is a powerful tool for taking local information to deduce global results, with applications across diverse areas including topology, group theory, analysis, general relativity and string theory. In these two introductory lectures
From playlist Oxford Mathematics Student Lectures - Riemannian Geometry

Poisson tensors in non-commutative gravity
In this video I go through my master thesis. You can find all the links discussed here: https://gist.github.com/Nikolaj-K/ce2dd6b6da0fbd791529bc8dd9183a74 Links: http://othes.univie.ac.at/16190/ https://arxiv.org/abs/1111.2732 https://www.linkedin.com/in/nikolaj-kuntner-0138aa104/ http
From playlist Physics

David Dos Santos Ferreira: The anisotropic Calderon problem
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Partial Differential Equations

Emanuel Milman: Functional Inequalities on sub-Riemannian manifolds via QCD
We are interested in obtaining Poincar ́e and log-Sobolev inequalities on domains in sub-Riemannian manifolds (equipped with their natural sub-Riemannian metric and volume measure). It is well-known that strictly sub-Riemannian manifolds do not satisfy any type of Curvature-Dimension condi
From playlist Workshop: High dimensional measures: geometric and probabilistic aspects
A. Belotto da Silva - Singular foliations in sub-Riemannian geometry and the Strong Sard Conjecture
Given a totally nonholonomic distribution of rank two $\Delta$ on a three-dimensional manifold $M$, it is natural to investigate the size of the set of points $\mathcal{X}^x$ that can be reached by singular horizontal paths starting from a same point $x \in M$. In this setting, the Sard co
From playlist Ecole d'été 2019 - Foliations and algebraic geometry

Understanding and computing the Riemann zeta function
In this video I explain Riemann's zeta function and the Riemann hypothesis. I also implement and algorithm to compute the return values - here's the Python script:https://gist.github.com/Nikolaj-K/996dba1ff1045d767b10d4d07b1b032f
From playlist Programming

Nijenhuis geometry for ECRs: Pre-recorded Lecture 4
Pre-recorded Lecture 4: Nijenhuis geometry for ECRs Date: 10 February 2022 Lecture slides: https://mathematical-research-institute.sydney.edu.au/wp-content/uploads/2022/02/Prerecorded_Lecture4.pdf ---------------------------------------------------------------------------------------------
From playlist MATRIX-SMRI Symposium: Nijenhuis Geometry and integrable systems

D. Prandri - Weyl law for singular Riemannian manifolds
In this talk we present recent results on the asymptotic growth of eigenvalues of the Laplace-Beltrami operator on singular Riemannian manifolds, where all geometrical invariants appearing in classical spectral asymptotics are unbounded, and the total volume can be infinite. Under suitable
From playlist Journées Sous-Riemanniennes 2018

Yoshihiro Ohnita: Minimal Maslov number of R-spaces canonically embedded in Einstein-Kähler C-spaces
An R-space is a compact homogeneous space obtained as an orbit of the isotropy representation of a Riemannian symmetric space. It is known that each R-space has the canonical embedding into a Kähler C-space as a real form which is a compact embedded totally geodesic Lagrangian submanifold.
From playlist Geometry

G. Molino - The Horizontal Einstein Property for H-Type sub-Riemannian Manifolds
We generalize the notion of H-type sub-Riemannian manifolds introduced by Baudoin and Kim, and then introduce a notion of parallel Clifford structure related to a recent work of Moroianu and Semmelmann. On those structures, we prove an Einstein property for the horizontal distribution usin
From playlist Journées Sous-Riemanniennes 2018

Joe Neeman: Gaussian isoperimetry and related topics II
The Gaussian isoperimetric inequality gives a sharp lower bound on the Gaussian surface area of any set in terms of its Gaussian measure. Its dimension-independent nature makes it a powerful tool for proving concentration inequalities in high dimensions. We will explore several consequence
From playlist Winter School on the Interplay between High-Dimensional Geometry and Probability